Khái niệm: Đường tiệm cận của một hàm số là một đường thẳng mà đồ thị của hàm số tiến đến càng gần khi giá trị của biến số tiến. Hướng dẫn giải - Bài 1.44 trang 48 SGK Toán 12 tập 1 - Cùng khám phá - Bài tập cuối chương 1. Cho hàm số \(y = \frac{{{x^2} + 7x + 3}}{{{x^2}}}\) có đồ thị là đường cong như Hình 1.70. Đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận? A. 1 . B. 2 . C...

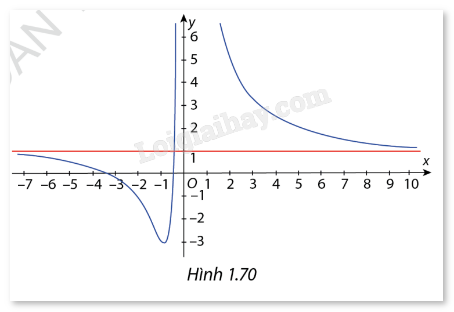
Cho hàm số \(y = \frac{{{x^2} + 7x + 3}}{{{x^2}}}\) có đồ thị là đường cong như Hình 1.70. Đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?
A. 1
B. 2
C. 3
D. 4
Advertisements (Quảng cáo)

Khái niệm: Đường tiệm cận của một hàm số là một đường thẳng mà đồ thị của hàm số tiến đến càng gần khi giá trị của biến số tiến ra vô cùng hoặc tiến tới một điểm đặc biệt nào đó nhưng không bao giờ chạm vào đường thẳng đó.

Nhìn vào đồ thị có thể thấy đồ thị hàm số có 1 tiệm cận ngang là \(y = 1\).
Ngoài ra đồ thị còn 1 tiệm cận đứng đó là \(x = 0\)
Vậy đồ thị hàm số có 2 đường tiệm cận. Chọn B.
