
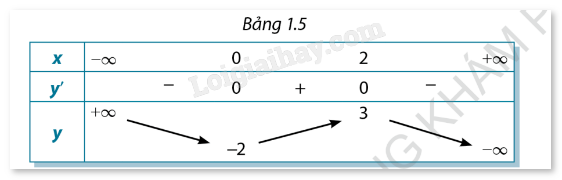
Cho hàm số \(y = f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như Bảng 1.5. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên \((0;2)\) và đạt cực đại tại \(x = 2\).
B. Hàm số đồng biến trên \((0;2)\) và đạt cực đại tại \(x = 0\).
C. Hàm số nghịch biến trên \((0;2)\) và đạt cực đại tại \(x = 2\).
Advertisements (Quảng cáo)
D. Hàm số nghịch biến trên \((0;2)\) và đạt cực đại tại \(x = 0\).

- Nếu trong một khoảng xác định, đạo hàm của hàm số mang dấu âm có nghĩa là hàm số nghịch biến trên khoảng đó. Ngược lại, nếu đạo hàm của hàm số mang dấu dương nghĩa là hàm số đồng biến trên khoảng đó.
- Điểm cực đại là điểm mà ngay tại đó, đồ thị hàm số chuyển từ đồng biến sang nghịch biến.

Dựa vào bảng 1.5 có thể thấy trong khoảng (0;2) thì hàm số đồng biến và đạt cực đại tại \(x = 2\). → Chọn A.
