
Trong Hoá học, cấu tạo của phân tử amoniac (\(N{H_3}\)) có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen (\(N\)) và đáy là tam giác \({H_1}{H_2}{H_3}\) với \({H_1}\), \({H_2}\), \({H_3}\) là vị trí của ba nguyên tử hydrogen (\(H\)). Góc tạo bởi liên kết \(H - N - H\), có hai cạnh là hai đoạn thẳng nối \(N\) với hai trong ba điểm \({H_1}\), \({H_2}\), \({H_3}\) (chẳng hạn như \({H_1}N{H_2}\)), được gọi là góc liên kết của phân tử \(N{H_3}\). Góc này xấp xỉ \({107^\circ }\).
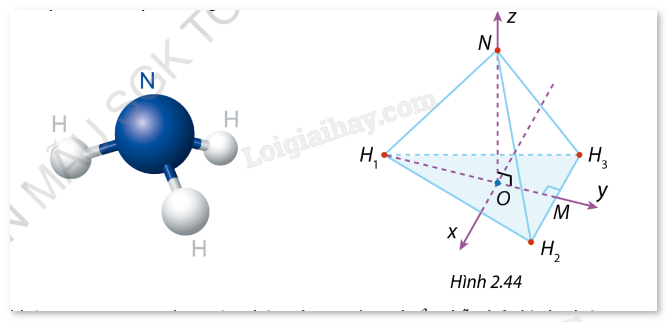
Trong không gian Oxyz, cho một phân tử \(N{H_3}\) được biểu diễn bởi hình chóp tam giác đều \(N.{H_1}{H_2}{H_3}\) với \(O\) là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm \(N\) thuộc trục Oz, ba nguyên tử hydrogen ở các vị trí \({H_1}\), \({H_2}\), \({H_3}\) trong đó \({H_1}(0; - 2;0)\) và \({H_2}{H_3}\) song song với trục Ox (Hình 2.44).
a) Tính khoảng cách giữa hai nguyên tử hydrogen.
b) Tính khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen (làm tròn các kết quả tính toán đến hàng phần trăm).

a) Sử dụng định lý sin trong công thức để tính khoảng cách giữa hai nguyên tử hydrogen (d) có góc bằng ∝.
\(d = 2R.\sin (\alpha )\)
b) Sử dụng công thức tính khoảng cách giữa hai điểm trong không gian:
\(d(N,{H_1}) = \sqrt {{{({x_{{H_1}}} - {x_N})}^2} + {{({y_{{H_1}}} - {y_N})}^2} + {{({z_{{H_1}}} - {z_N})}^2}} \)
Thay các tọa độ tương ứng để tính khoảng cách \(d(N,{H_1})\), \(d(N,{H_2})\), \(d(N,{H_3})\).

a)
Advertisements (Quảng cáo)
Bởi vì tam giác \({H_1}{H_2}{H_3}\) là tam giác đều nên áp dụng vào định lý sin trong tam giác, ta có:
\({H_1}{H_2} = {H_1}{H_3} = {H_2}{H_3} = 2R\sin {60^\circ } = \sqrt 3 R\)
Trong trường hợp này, O là trọng tâm của tam giác \({H_1}{H_2}{H_3}\) và O cũng là bán kính đường tròn ngoại tiếp nên \(R = 2\), ta có: \(d = 2\sqrt 3 \)
b) Để tính khoảng cách giữa nguyên tử nitrogen \(N(0;0;z)\) với nguyên tử hydrogen \({H_1}(0; - 2;0)\), ta sử dụng công thức:
\(N{H_1} = \sqrt {{{(0 - 0)}^2} + {{(0 + 2)}^2} + {{(z - 0)}^2}} = \sqrt {4 + {z^2}} \)
Vì khoảng cách từ gốc toạ độ O đến \({H_2}\) là 2, do đó \({H_2}\) có toạ độ là
\({H_2}(2\cos \theta ;2\sin \theta ;0)\)
Với θ là góc \(\widehat {xO{H_2}}\). Và vì \({H_1}{H_2}{H_3}\) là tam giác đều nên \(\widehat {xO{H_2}} = 30^\circ \).
Vậy \({H_2}\) có toạ độ là: \({H_2}(\sqrt 3 ;1;0)\)
Toạ độ của vectơ \(\overrightarrow {N{H_1}} ,\overrightarrow {N{H_2}} \)là:
\(\overrightarrow {N{H_1}} = \left( {0; - 2; - z} \right),\overrightarrow {N{H_2}} = \left( {\sqrt 3 ;1; - z} \right)\)
Từ đó ta có \(z\): \(\cos {107^\circ } = \frac{{\overrightarrow {N{H_1}} .\overrightarrow {N{H_2}} }}{{\left| {\overrightarrow {N{H_1}} } \right|.\left| {\overrightarrow {N{H_2}} } \right|}} = \frac{{ - 2 + {z^2}}}{{4 + {z^2}}}\)
Suy ra: \( - 2 + {z^2} = \left( {4 + {z^2}} \right).\cos 107^\circ \Leftrightarrow 0,71{z^2} = 0,83 \Rightarrow z = 1,08\).
