Câu hỏi/bài tập:
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau đây:
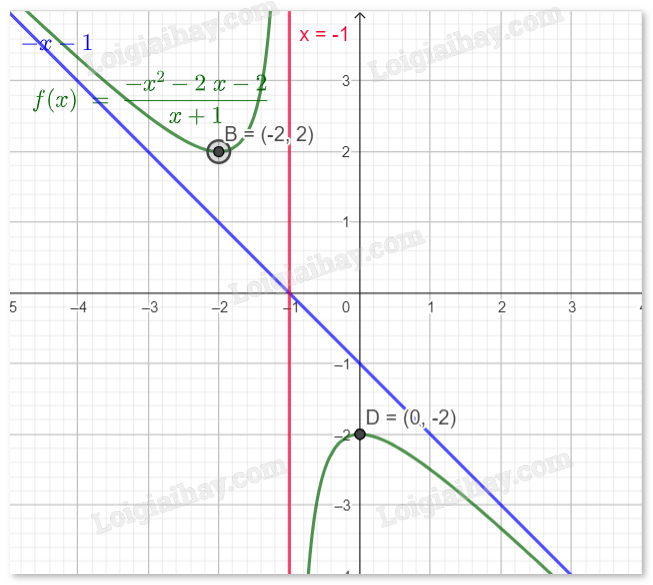
a) \(y = \frac{{ - {x^2} - 2x - 2}}{{x + 1}}\)
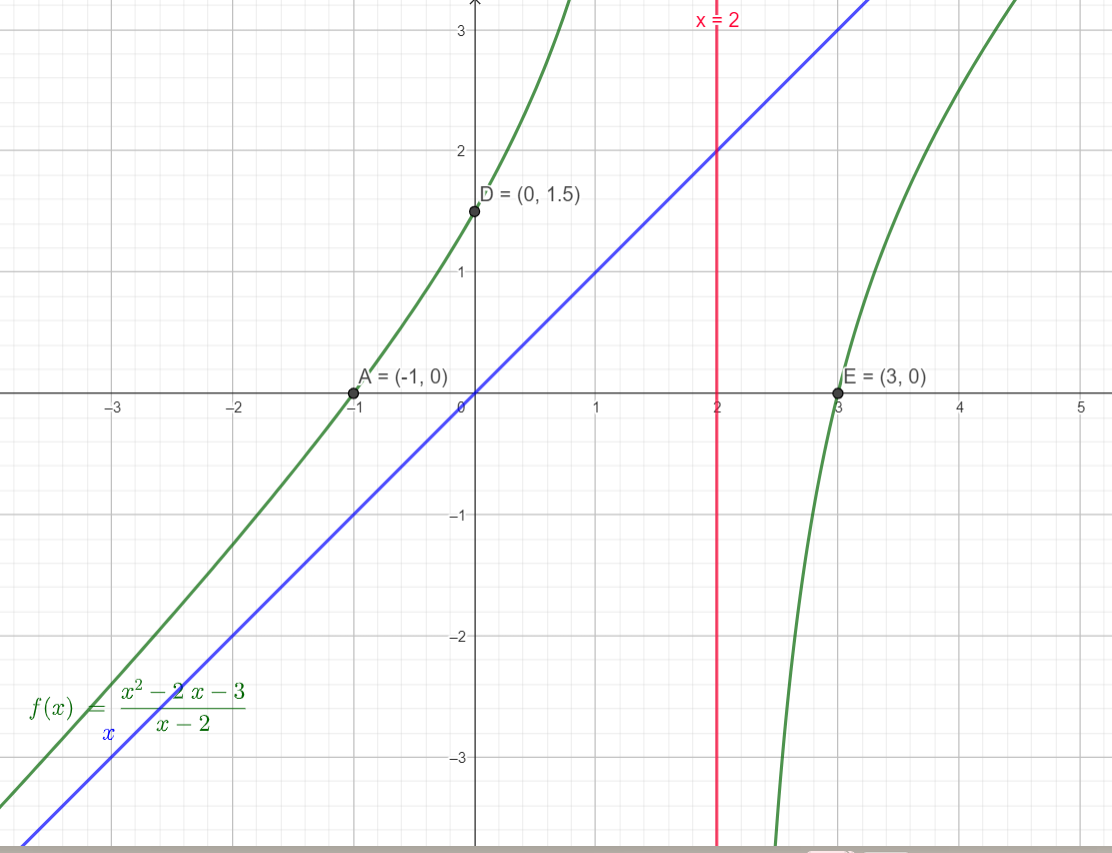
b) \({\rm{y}} = \frac{{{x^2} - 2x - 3}}{{x - 2}}\)

- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.

a)
- Tập xác định: D = R \ {-1}.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = - \infty .\)
\(\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = \infty .\)
Suy ra x = -1 là tiệm cận đứng của hàm số.
\(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to \infty } [ - (x + 1)] - 0 = - \infty \).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - \infty } [ - (x + 1)] - 0 = \infty \).
Suy ra hàm số không có tiệm cận ngang
\(\frac{{ - {x^2} - 2x - 2}}{{x + 1}} = - x - 1 + \frac{{ - 1}}{{x + 1}}\) (Sử dụng phép chia đa thức)
Khi \(x \to \pm \infty ,\frac{{ - 1}}{{x + 1}} \to 0\) nên \(y = - x - 1\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = \frac{{ - (2x + 2)(x + 1) + \left( {{x^2} + 2x + 2} \right)}}{{{{(x + 1)}^2}}} = \frac{{ - {x^2} - 2x}}{{{{(x + 1)}^2}}}\).
\({y^\prime } = 0 \leftrightarrow - {x^2} - 2x \leftrightarrow - x(x + 2) = 0 \leftrightarrow x = 0,{\rm{ }}x = - 2\).
Bảng biến thiên:
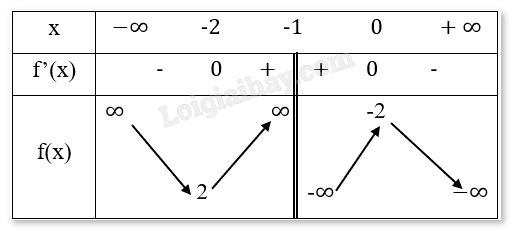
Chiều biến thiên: Hàm số nghịch biến trên các khoảng (−∞,-2) và (-1,0), đồng biến trên khoảng (-2,-1) và (-1,0).
Cực trị: Hàm số đạt cực tiểu tại \(x = - 2,{y_{CT}} = 2\).
Hàm số đạt cực đại tại \(x = 0,{y_{CD}} = - 2\).
Advertisements (Quảng cáo)
- Vẽ đồ thị:
Tiệm cận đứng \({\rm{x}} = - 1\), tiệm cận xiên \(y = - x - 1\).
Giao điểm với trục Oy là \((0, - 2)\).
b)
- Tập xác định: D = R \ {2}.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to 2 + } y = \mathop {\lim }\limits_{x \to 2 + } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \).
\(\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \).
Suy ra x = 2 là tiệm cận đứng của hàm số.
\(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \).
Suy ra hàm số không có tiệm cận ngang
\(\frac{{{x^2} - 2x - 3}}{{x - 2}} = x + \frac{{ - 3}}{{x + 1}}\) .
Khi \(x \to \pm \infty ,\frac{{ - 3}}{{x + 1}} \to 0\) nên \(y = x\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = \frac{{(2x - 2)(x - 2) - \left( {{x^2} - 2x - 3} \right)}}{{{{(x - 2)}^2}}} = \frac{{{x^2} - 4x + 7}}{{{{(x - 2)}^2}}} > 0\forall x \in D\).
Vậy hàm số đồng biến trên tập xác định.
Bảng biến thiên:
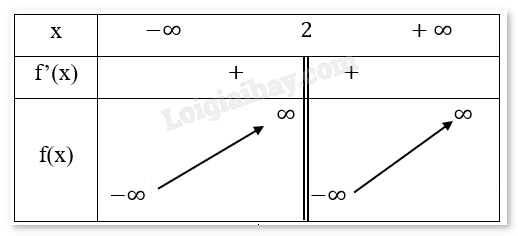
Chiều biến thiên: Hàm số đồng biến trên khoảng (-\(\infty ,2\)) và (2,\(\infty \)).
Cực trị: Hàm số không có cực trị.
- Vẽ đồ thị:
Tiệm cận đứng x = 2, tiệm cận xiên y = x.
Giao điểm với trục Oy là (0,\(\frac{3}{2}\)).
Giao điểm với trục Ox là (-1,0) và (3,0).