Hoạt động (HĐ) 2
Cho hàm số \(y = \frac{x^2{{} + 4}}{x}\)
a) Xét tính liên tục của hàm số đã cho trên mỗi đoạn\([ - 5; - 1]\) và \([ - 4;3]\)
b) Tính giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của hàm số đã cho trên các đoạn\([ - 5; - 1]\) và \([ - 4;3]\)

a) Tìm tập xác định của hàm số
b) Bước 1: Tính \(y’\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định giá trị lớn nhất, giá trị bé nhất của hàm số trên các đoạn

a) TXĐ: \(x \in R/\{ 0\} \)
Vậy hàm số liên tục trên đoạn \([ - 5; - 1]\)
Và không liên tục trên đoạn \([ - 4;3]\)
Ta có \(y’ = \frac{{{x^2} - 4}}{{{x^2}}}\)
Xét \(y’ = 0\) \( \Rightarrow {x^2} - 4 = 0\)\( \Rightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
Từ đó ta có bảng biến thiên là
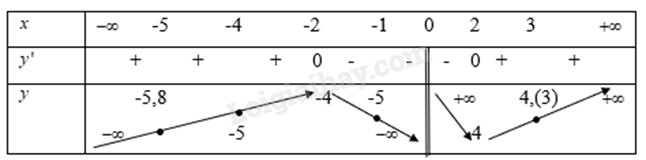
b) Từ bảng biến thiên ta có
Hàm số\ (y = \frac{{{x^2} + 4}}{x}\) đạt giá trị lớn nhất trên khoảng\([ - 5; - 1]\) tại \(x = 1\) khi đó
Hàm số \(y = \frac{{{x^2} + 4}}{x}\) đạt giá trị bé nhất trên khoảng\([ - 5; - 1]\) tại điểm \(x = - 5\) khi đó
Hàm số \(y = \frac{{{x^2} + 4}}{x}\) đạt giá trị lớn nhất \([ - 4;3]\) trên khoảng tại điểm
Hàm số \(y = \frac{{{x^2} + 4}}{x}\) đạt giá trị bé nhất \([ - 4;3]\) trên khoảng tại điểm
Hoạt động (HĐ) 3
Cho hàm số \(y = f(x)\) liên tục trên đoạn, có đạo hàm trên các khoảng \(( - 3;1)\)và \((1;6)\) có dồ thị hàm số như hình 1.9, biết rằng \(f( - 3) = - 5\) và \(f(6) = - 2\)
a) Xác định các điểm cực trị thuộc đoạn \([ - 3;6]\) của hàm số
Advertisements (Quảng cáo)
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \([ - 3;6]\)
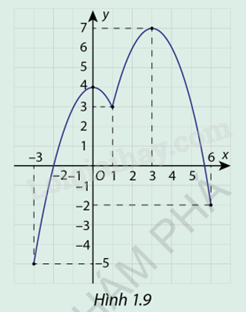

Dựa vào đồ thị hàm số (hình 1.9) rồi nhận xét

a) Dựa vào đồ thị hàm số, ta thấy
Đồ thị hàm số có các điểm cực trị là \(x = - 3\), \(x = 0\), \(x = 1\),\(x = 3\), \(x = 6\)
b) Hàm số đạt giá trị lớn nhất trên khoảng \([ - 3;6]\) tại \(x = 3\)
Hàm số đạt giá trị nhỏ nhất trên khoảng \([ - 3;6]\) tại \(x = - 3\)
Luyện tập (LT) 3
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y = \frac{{x + 2}}{{x - 1}}\) trên đoạn \([2;4]\)

Bước 1 Tính \(y’\)
Bước 2 Lập bảng biến thiên
Bước 3 Suy ra điểm có giá trị lớn nhất, điểm có giá trị bé nhất của hàm số trên đoạn \([2;4]\)

Hàm số trên xác định trên R/{1}
Ta có \(y’ = \frac{{ - 3}}{{{{(x - 1)}^2}}}\)
Vì \(y’
Nên hàm số luôn nghịch biến
Khi đó ta có bảng biến thiên là
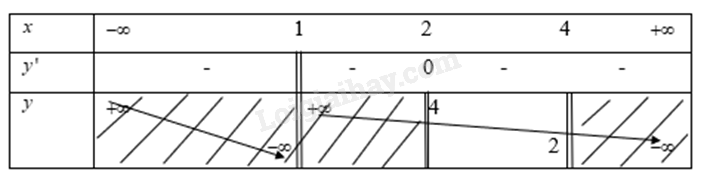
Từ bảng biến thiên ta thấy
Hàm số y đạt giá trị lớn nhất tại x = 2 khi đó y = 4
Hàm số y đạt giá trị lớn nhất tại x = 4 khi đó y = 2
