Hoạt động (HĐ) 2
Nhắc lại các khái niệm liên quan đến vectơ trong mặt phẳng:
- Độ dài của vectơ.
- Giá của vectơ.
- Hai vectơ cùng phương, hai vectơ cùng hướng.
- Hai vectơ bằng nhau.
- Hai vectơ đối nhau.
- Vectơ-không.

Các khái niệm liên quan đến vectơ trong không gian có trong Sách giáo khoa trang 52.

- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của nó. Độ dài của vectơ \(\vec a\) được kí hiệu là \(|\vec a|\).
- Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
- Hai vectơ được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. Vectơ đối của \(\vec a\) được kí hiệu là \( - \vec a\).
- Vectơ-không có độ dài bằng 0 và cùng phương, cùng hướng với mọi vectơ.
Luyện tập (LT) 2
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\).
a) Trong các vectơ khác \(\vec 0\), có điểm đầu và̀ điểm cuối là các đỉnh của hình hộp, hãy chỉ ra những vectơ:
Advertisements (Quảng cáo)
- Cùng phương với vectơ \(\overrightarrow {AB} \);
- Bä̀ng vectơ \(\overrightarrow {AB} \);
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \).
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \) trong trường hợp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, có \(A{A^\prime } = \) a, \(AB = b,BC = c\) và \(\widehat {ABC} = {120^o}\).

a) Xác định các vectơ theo yêu cầu đề bài dựa trên lý thuyết về vectơ.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
b) Sử dụng công thức và định lý để tính độ dài của vectơ.

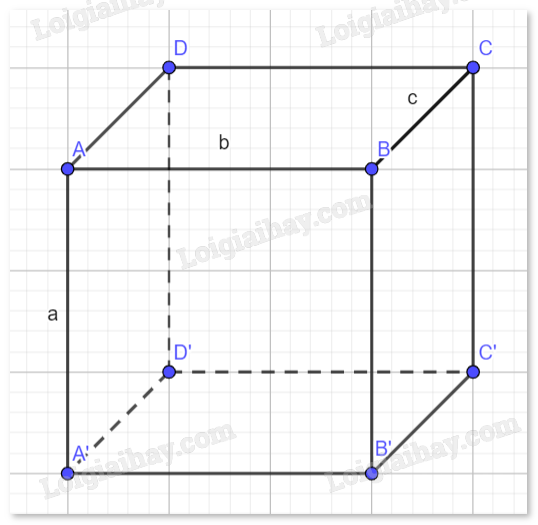
a) Các vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp:
- Cùng phương với vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {{A^\prime }{B^\prime }} \), \(\overrightarrow {DC} \), \(\overrightarrow {{D^\prime }{C^\prime }} \),\(\overrightarrow {{B^\prime }{A^\prime }} \), \(\overrightarrow {CD} \), \(\overrightarrow {{C^\prime }{D^\prime }} \),\(\overrightarrow {BA} \)
- Bằng vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {AB} = \overrightarrow {{A^\prime }{B^\prime }} = \overrightarrow {DC} = \overrightarrow {{D^\prime }{C^\prime }} \)
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \): \(\overrightarrow {{B^\prime }B} \),\(\overrightarrow {{C^\prime }C} \),\(\overrightarrow {{D^\prime }D} \),\(\overrightarrow {{A^\prime }A} \)
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \):
- Vì \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, suy ra tam giác \(AA’C’\) vuông tại \(A’\). Từ đó ta có:
\(\begin{array}{l}AC’ = \sqrt {{{(AA’)}^2} + {{(A’C’)}^2}} = \sqrt {{a^2} + A{C^2}} = \sqrt {{a^2} + (A{B^2} + B{C^2} - 2.AB.BC.\cos (120^\circ )} \\AC’ = \sqrt {{a^2} + {b^2} + {c^2} - 2bc.\left( { - \frac{1}{2}} \right)} = \sqrt {{a^2} + {b^2} + {c^2} - bc} \end{array}\)
Vậy độ dài của vectơ \(\overrightarrow {A{C^\prime }} \)là: \(\sqrt {{a^2} + {b^2} + {c^2} - bc} \)
