Hoạt động (HĐ) 2
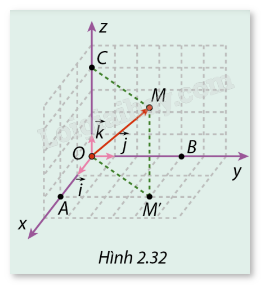
Cho điểm trong không gian Oxyz. Trong ba mặt phẳng tọa độ là ba lưới ô vuông có cạnh bằng đơn vị. Biết rằng , và vị trí các điểm M’, A, B, C được cho như trong Hình 2.32.
a) Biếu diễn theo hai vecto và .
b) Biểu diễn theo hai vecto đơn vị .
c) Biểu diễn theo ba vectơ dơn vị .

Sử dụng các định nghĩa, các quy tắc về vectơ trong không gian và mối quan hệ trực giao giữa các mặt phẳng tọa độ để biểu diễn các vectơ theo các vectơ đơn vị.

a) Biểu diễn \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OM’} \) và \(\overrightarrow {OC} \):
Do \(MM’ \bot (Oxy)\), \(MC \bot Oz\) nên OCMM’ là hình chữ nhật.
Áp dụng quy tắc hình bình hành vào hình chữ nhật OCMM’, ta có:
\(\overrightarrow {OM} = \overrightarrow {OM’} + \overrightarrow {OC} \)
b) Biểu diễn \(\overrightarrow {OM’} \) theo hai vectơ đơn vị \(\vec i,\vec j\):
Áp dụng quy tắc hình bình hành vào hình chữ nhật OAM’B, ta có:
\(\overrightarrow {OM’} = \overrightarrow {OA} + \overrightarrow {OB} \)
Mà \(\overrightarrow {OA} = 2\overrightarrow i ,\overrightarrow {OB} = 4\overrightarrow j \) nên:
\(\overrightarrow {OM’} = 2\overrightarrow i + 4\overrightarrow j \)
c) Biểu diễn \(\overrightarrow {OM} \) theo ba vectơ đơn vị \(\vec i,\vec j,\vec k\):
Từ câu a, b ta có:
\(\overrightarrow {OM} = \overrightarrow {OM’} + \overrightarrow {OC} \) và \(\overrightarrow {OM’} = 2\overrightarrow i + 4\overrightarrow j \)
Lại có \(\overrightarrow {OC} = 4\overrightarrow k \) nên:
\(\overrightarrow {OM} = 2\vec i + 4\vec j + 4\vec k\)
Luyện tập (LT) 2
Trong không gian Oxyz, cho ba điểm A(1;0;9), B(6;1;0) và C(0;0;1). Gọi G là trọng tâm của tam giác ABC. Tìm toạ độ điểm G.

Trọng tâm của tam giác là trung bình cộng tọa độ của ba đỉnh của tam giác. Nếu các đỉnh của tam giác là \(A({x_1},{y_1},{z_1})\), \(B({x_2},{y_2},{z_2})\), và \(C({x_3},{y_3},{z_3})\), tọa độ của trọng tâm G được tính bằng:
Advertisements (Quảng cáo)
\(G\left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\frac{{{y_1} + {y_2} + {y_3}}}{3},\frac{{{z_1} + {z_2} + {z_3}}}{3}} \right)\)

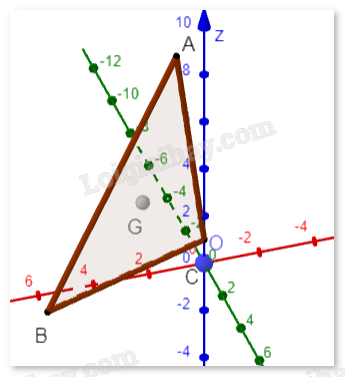
Toạ độ của điểm trọng tâm G là trung bình cộng của toạ độ các điểm A, B, C.
\({x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 + 6 + 0}}{3} = \frac{7}{3}\)
\({y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{0 + 1 + 0}}{3} = \frac{1}{3}\)
\({z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{9 + 0 + 1}}{3} = \frac{{10}}{3}\)
Toạ độ của trọng tâm G là: \(G\left( {\frac{7}{3},\frac{1}{3},\frac{{10}}{3}} \right)\)
Luyện tập (LT) 3
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có \[\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AA’} \] theo thứ tự cùng hướng với các vectơ đơn vị \(\vec i,\vec j,\vec k\) và có \(AB = a,AD = b,AA’ = c\). Gọi M là trung điểm cạnh CC’. Hãy xác định toạ độ các điểm B, C, C’ và M.

Xác định tọa độ điểm cơ bản: Sử dụng các vectơ đơn vị để xác định tọa độ của các điểm quan trọng trong không gian.
Xác định tọa độ các điểm còn lại: Tính tọa độ của các điểm đối diện trong hình hộp dựa trên tọa độ của các điểm đã biết.
Tính tọa độ trung điểm: Sử dụng công thức tính trung điểm để tìm tọa độ của điểm trung gian trên cạnh.

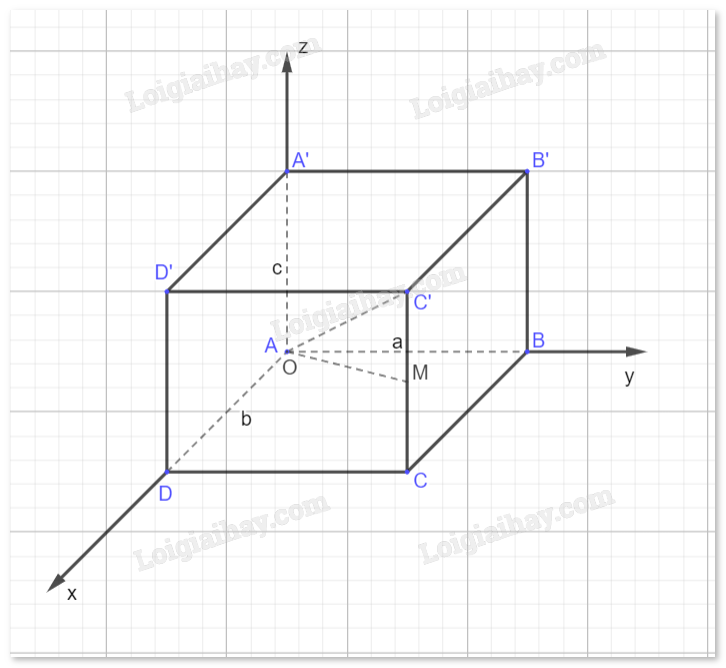
- Xác định tọa độ các điểm cơ bản:
Tọa độ của điểm A là (0, 0, 0) vì A trùng với gốc tọa độ O.
Tọa độ của điểm B: Điểm B nằm cách điểm A một đoạn a theo hướng của vector đơn vị \(\vec i\). Vì vậy, tọa độ của B là (a, 0, 0).
Tọa độ của điểm D: Điểm D nằm cách điểm A một đoạn b theo hướng của vector đơn vị \(\vec j\). Vì vậy, tọa độ của D là (0, b, 0).
Tọa độ của điểm A’: Điểm A’ nằm cách điểm A một đoạn c theo hướng của vector đơn vị \(\vec k\). Vì vậy, tọa độ của A’ là (0, 0, c).
- Xác định tọa độ các điểm còn lại:
Tọa độ của điểm C: Điểm C nằm đối diện với điểm A trong hình hộp và nằm trên mặt phẳng chứa B và D. Vì vậy, tọa độ của C là (a, b, 0).
Tọa độ của điểm C’: Điểm C’ nằm đối diện với điểm A’ trong hình hộp và nằm trên mặt phẳng chứa B’ và D’. Vì vậy, tọa độ của C’ là (a, b, c).
Trung điểm của đoạn thẳng CC’ có tọa độ trung bình của tọa độ C và C’. Tọa độ của C là (a, b, 0) và tọa độ của C’ là (a, b, c). Do đó, tọa độ của M là:
\(M = \left( {\frac{{a + a}}{2},\frac{{b + b}}{2},\frac{{0 + c}}{2}} \right) = (a,b,\frac{c}{2})\)
