Luyện tập (LT) 4
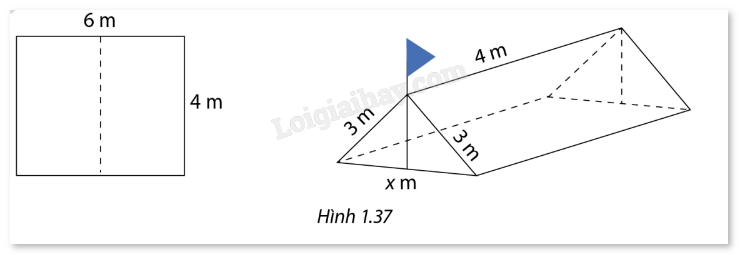
Trong đợt chào mừng kỷ niệm ngày 26 tháng 3, trường X có tổ chức cho các lớp bày các gian hàng tại sân trường. Để có thể che nắng, chứa đồ đạc trong quá trình tham gia hoạt động, một lớp đã nghĩ ra ý tưởng như sau: Dựng trên mặt đất bằng phẳng một chiếc lều từ một tấm bạt hình chữ nhật có chiều rộng là 4m và chiều dài là 6m, bằng cách gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh là chiều dài của tấm bạt, hai mép chiều rộng còn lại của tấm bạt sát đất và cách nhau x (m). Tìm x để khoảng không gian phía trong lều là lớn nhất.

- Xác định công thức thể tích khối hình học.
- Thiết lập hàm thể tích theo biến x.
- Tìm giá trị lớn nhất của hàm thể tích.

Khi tấm bạt được gập đôi, hình dạng của lều sẽ là một lăng trụ tam giác đều với chiều cao là 4m và đáy là tam giác có 2 cạnh bên là 3m. Hai mép của chiều rộng 4m chạm đất và khoảng cách giữa chúng là x.
Gọi chiều cao của tam giác đáy là \({h_{{\rm{day }}}}:{h_{day}} = \sqrt {9 - {{\left( {\frac{x}{2}} \right)}^2}} \).
Tam giác đáy của hình lăng trụ có diện tích là: \(s = \frac{1}{2} \cdot x \cdot \sqrt {9 - {{\left( {\frac{x}{2}} \right)}^2}} \).
Thể tích của hình lăng trụ là: \(V = S \cdot h = \frac{1}{2} \cdot x \cdot \sqrt {9 - {{\left( {\frac{x}{2}} \right)}^2}} \cdot 4 = 2x \cdot \sqrt {9 - {{\left( {\frac{x}{2}} \right)}^2}} = \sqrt {36{x^2} - {x^4}} \).
Ta có hàm số: \(y = \sqrt {36{x^2} - {x^4}} \).
\({y^\prime } = \frac{{ - 4{x^3} + 72x}}{{2\sqrt {36{x^2} - {x^4}} }} = \frac{{ - 2{x^3} + 36x}}{{\sqrt {36x - {x^2}} }}\).
\({y^\prime } = 0 \Leftrightarrow - 2{x^3} + 36x = 0 \Rightarrow x = - 3\sqrt 2 \) hoăc \(x = 0\) hoặc \(x = 3\sqrt 2 \).
Do \(x > 0\) nên chỉ có \(x = 3\sqrt 2 \) thoả mãn.
Nhận thấy y đồng biến trên khoảng \((0,3\sqrt 2 )\) vậy nên giá trị tại \(x = 3\sqrt 2 \) là lớn nhất.
Kết luận: Giá trị \(x = 3\sqrt 2 \) m là giá trị làm cho thể tích của lều là lớn nhất.
Luyện tập (LT) 5
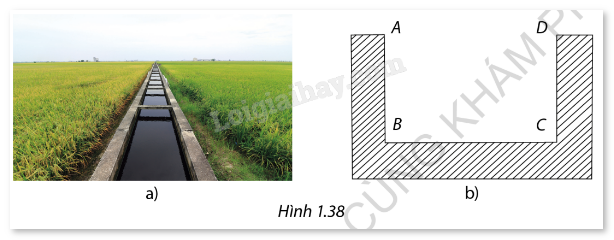
Hình 1.38a là một mương dẫn nước thủy lợi tại một địa phương. Phần không gian trong mương để nước chảy có mặt cắt ngang là một hình chữ nhật ABCD (Hình 1.36b). Với điều kiện lưu lượng nước qua mương cho phép ở đây thì diện tích mặt cắt ABCD là 1,2m2. Để đảm bảo yêu cầu kỹ thuật tốt nhất cho mương, người ta cần thiết kế sao cho tổng độ dài AB+BC+CD là ngắn nhất.
a) Đặt BC= x, tính y=AB+BC+CD theo x.
b) Khảo sát hàm số y=f(x) tìm được ở câu a, từ đó tính x để y nhỏ nhất, biết rằng theo quy định thì đoạn BC (chiều rộng đáy mương) phải dưới 10 m.

a) Sử dụng công thức diện tích để thiết lập phương trình liên hệ giữa các biến.
Biểu diễn tổng chiều dài cần tối thiểu hóa theo biến ?.
b) Khảo sát sự biến thiên của hàm số.
Tìm giá trị ? để hàm số đạt giá trị nhỏ nhất trong khoảng xác định.

a) Gọi \({\rm{AB}} = {\rm{CD}} = {\rm{h}}\). Ta có diện tích hình chữ nhật ABCD là:
\(S = BC \cdot AB = x.h = 1,2\;{{\rm{m}}^2}\).
Từ đó suy ra \(h = \frac{{1,2}}{x}\).
Tổng chiều dài cần tối thiểu hóa là: \(y = AB + BC + CD = h + x + h = 2h + x\).
Thay \(h = \frac{{1,2}}{x}\) vào, ta được: \(y = 2 \cdot \frac{{1,2}}{x} + x = \frac{{2,4}}{x} + x\).
b) Khảo sát hàm số \(y = f(x) = \frac{{2,4}}{x} + x\).
- Tập xác định: \(D = \{ x > 0,x \in R\} \).
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to 0 + } y = \mathop {\lim }\limits_{x \to {0^ + }} \left( {\frac{{2,4}}{x} + x} \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {\frac{{2,4}}{x} + x} \right) = \infty \).
\(\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} \left( {\frac{{2,4}}{x} + x} \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {\frac{{2,4}}{x} + x} \right) = - \infty \).
Suy ra \({\rm{x}} = 0\) là tiệm cận đứng của hàm số.
Khi \(x \to \pm \infty ,\frac{{2,4}}{x} \to 0\) nên \(y = x\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = - \frac{{2,4}}{{{x^2}}} + 1\).
\({y^\prime } = 0 \Rightarrow - \frac{{2,4}}{{{x^2}}} + 1 = 0 \Rightarrow \frac{{2,4}}{{{x^2}}} = 1 \Rightarrow x = 2,4\) vì \(x > 0.\)
Advertisements (Quảng cáo)
Bảng biến thiên:
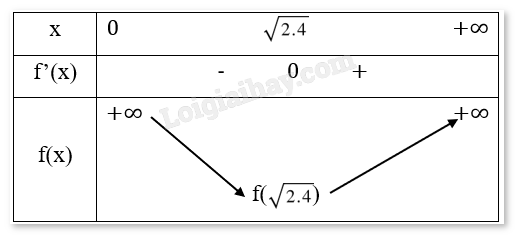
Cực trị: Hàm số đạt cực tiểu tại \(x = \sqrt {2,4} \).
Vậy để tổng chiều dài AB+BC+CD là ngắn nhất, ta chọn: \(x = \sqrt {2,4} \approx 1,55\;{\rm{m}}.\)
Vận dụng (VD) 3
Khởi động: Một cửa hàng kinh doanh điện thoại di động đã ký hợp đồng với nơi sản xuất để nhập về 2.500 điện thoại trong một năm. Cửa hàng có thể nhập về tất cả số điện thoại này và bán dần, tuy nhiên như vậy sẽ tốn nhiều chi phí cho lưu kho, bảo quản và mặt bằng. Vì vậy họ được phép nhập về theo từng đợt, mỗi đợt đều nhập x chiếc điện thoại, sau đó sẽ lưu trữ ở kho hàng một nửa số điện thoại đó. Biết rằng kinh phí cho việc lưu trữ ở kho trong một năm là 100.000 đồng trên một chiếc điện thoại (chỉ tính trong đợt nhập đầu tiên), chi phí cho mỗi đợt nhập hàng (vận chuyển, giấy tờ, nhân công sắp xếp,...) cố định là 200.000 đồng và thêm 90.000 đồng trên mỗi điện thoại. Bằng cách xác định hàm số biểu thị sự phụ thuộc của tổng chi phí vào số điện thoại nhập trong mỗi đợt và khảo sát sự biến thiên của hàm số này, người ta có thể tìm được phương án nhập điện thoại để tổng chi phí là nhỏ nhất. Họ đã làm điều đó như thế nào?
Trở lại phần khởi động đầu bài.
a) Lập công thức hàm số tổng chi phí lưu kho và nhập hàng, khảo sát sự biến thiên của hàm số này.
b) Tìm số đợt nhập và số điện thoại nhập trong mỗi đợt để tổng chi phí của câu a là nhỏ nhất.


1. Lập công thức hàm số tổng chi phí:
- Đặt ? là số điện thoại nhập trong mỗi đợt.
- Tính số đợt nhập cần thiết trong một năm là \(\frac{{2500}}{x}\).
- Xác định các thành phần chi phí:
+ Chi phí cố định cho mỗi đợt nhập hàng.
+ Chi phí trên mỗi điện thoại.
+ Chi phí lưu kho.
- Tổng hợp các chi phí để tạo thành công thức tổng chi phí.
2. Khảo sát sự biến thiên của hàm số tổng chi phí:
- Tính đạo hàm của hàm số tổng chi phí.
- Tìm các điểm tới hạn bằng cách giải phương trình đạo hàm bằng 0.
- Xác định các giá trị biên và sử dụng đạo hàm để tìm giá trị nhỏ nhất của hàm số.
3. Tìm số đợt nhập và số điện thoại nhập trong mỗi đợt:
Sử dụng kết quả từ khảo sát hàm số để xác định số đợt nhập và số điện thoại nhập trong mỗi đợt sao cho tổng chi phí là nhỏ nhất.

a) Gọi x là số điện thoại nhập trong mỗi đợt. Ta có:
- Số đợt nhập hàng trong một năm là \(\frac{{2500}}{x}\).
- Chi phí cố định cho mỗi đợt nhập hàng là 200.000 đồng.
- Chi phí trên mỗi điện thoại là 90.000 đồng.
- Chi phí lưu kho cho mỗi điện thoại là 100.000 đồng trong một năm.
Tổng chi phí cho mỗi đợt nhập hàng là: \(c = 200000 + 90000x\).
Tổng chi phí lưu kho cho \(x\) điện thoại trong một năm là: \(\kappa = 100000x\).
Vậy tổng chi phí cho mỗi đợt là: \(T(x) = (200000 + 90000x) \cdot \frac{{2500}}{x} + 100000x\).
Ta có: \(T(x) = \frac{{2500.200000}}{x} + 2500.90000 + 100000x\).
\(T(x) = \frac{{500000000}}{x} + 225000000 + 100000x\).
b) Khảo sát sự biến thiên của hàm số tổng chi phí.
Ta có hàm số: \(T(x) = \frac{{500000000}}{x} + 225000000 + 100000x\).
Tính đạo hàm: \({T^\prime }(x) = \frac{{ - 500000000}}{{{x^2}}} + 100000\).
Giải phương trình \({{\rm{T}}^\prime }({\rm{x}}) = 0\) :
\(\frac{{ - 500000000}}{{{x^2}}} + 100000 = 0 \Leftrightarrow 100000 = \frac{{500000000}}{{{x^2}}} \Leftrightarrow {x^2} = 5000 \Leftrightarrow x = \sqrt {5000} \approx 70.71.\)
Vậy số điện thoại nhập trong mỗi đợt là \(x \approx 70.71\). Số đợt nhập là \(\frac{{2500}}{{70.71}} \approx 35.37\).
Kết luận: Cửa hàng nên nhập khoảng 71 điện thoại mỗi đợt và có khoảng 35 đợt nhập để tổng chi phí là nhỏ nhất.
