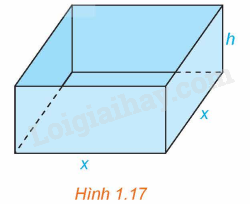
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng \(108c{m^2}\) như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
Sử dụng kiến thức về cách tìm giá trị lớn nhất của hàm số trên một đoạn để tính: Giả sử \(y = f\left( x \right)\) là hàm số liên tục trên \(\left[ {a;b} \right]\) và có đạo hàm trên (a; b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn \(\left[ {a;b} \right]\) mà đạo hàm \(f’\left( x \right) = 0\).
Các bước tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {a;b} \right]\):
1. Tìm các điểm \({x_1},{x_2},...{x_n} \in \left( {a;b} \right)\), tại đó \(f’\left( x \right) = 0\) hoặc không tồn tại.
2. Tính \(f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right)\), f(a) và f(b).
3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
\(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\)
Hình hộp trên có độ dài cạnh đáy là x (cm, \(x > 0\)) và chiều cao là h (cm, \(h > 0\))
Diện tích bề mặt của hình hộp là \(108c{m^2}\) nên \({x^2} + 4xh = 108 \Rightarrow h = \frac{{108 - {x^2}}}{{4x}}\left( {cm} \right)\)
Thể tích của hình hộp là: \(V = {x^2}.h = {x^2}.\frac{{108 - {x^2}}}{{4x}} = \frac{{108x - {x^3}}}{4}\left( {c{m^3}} \right)\)
Ta có: \(V’ = \frac{{ - 3{x^2} + 108}}{4},V’ = 0 \Leftrightarrow x = 6\) (do \(x > 0\))
Bảng biến thiên:
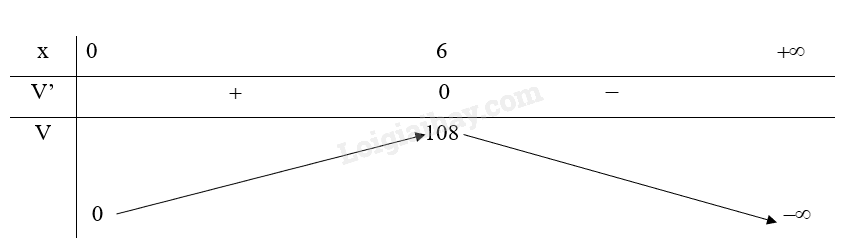
Do đó, thể tích của hình hộp là lớn nhất khi độ dài cạnh đáy \(x = 6\)cm
Khi đó, chiều cao của hình hộp là: \(\frac{{108 - {6^2}}}{{4.6}} = 3\left( {cm} \right)\).