Bài 1.16 trang 25 Toán 12 tập 1 - Kết nối tri thức: Hình 1.26 là đồ thị của hàm số $y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}$...

Hình 1.26 là đồ thị của hàm số $y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}$

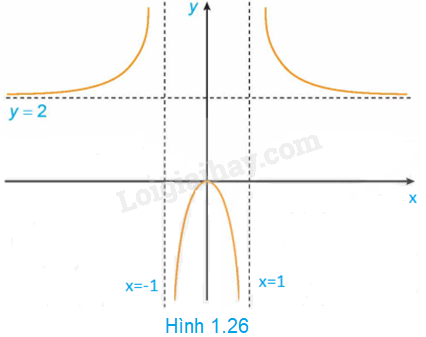
Sử dụng đồ thị này, hãy:a) Viết kết quả của các giới hạn sau: $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)$; $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)$; $\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)$; $\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)$b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.

Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng $y = {y_0}$ gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số $y = f\left( x \right)$ nếu $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}$ hoặc $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}$

Sử dụng kiến thức về khái niệm tiệm cận đứng của đồ thị hàm số để tìm tiệm cận đứng: Đường thẳng $x = {x_0}$ gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số $y = f\left( x \right)$ nếu ít nhất một trong các điều kiện sau được thỏa mãn: $\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty$; $\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty$; $\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty$; $\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty$

a) $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2$; $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2$; $\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = - \infty$; $\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = - \infty$

b) Do đó, tiệm cận đứng của đồ thị hàm số là $x = 1;x = - 1$.

Tiệm cận ngang của đồ thị hàm số là $y = 2$