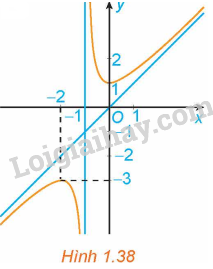
Đồ thị trong Hình 1.38 là đồ thị của hàm số:
A. \(y = x - \frac{1}{{x + 1}}\).B. \(y = \frac{{2x + 1}}{{x + 1}}\).C. \(y = \frac{{{x^2} - x + 1}}{{x + 1}}\).D. \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\).
Sử dụng kiến thức về điểm thuộc đồ thị hàm số, dạng của đồ thị hàm số, tiệm cận của đồ thị hàm số để tìm đồ thị hàm số đúng.
Đồ thị hàm số trong hình 1.38 có dạng: \(y = \frac{{a{x^2} + bx + c}}{{px + q}}\left( {a \ne 0,p \ne 0} \right)\) và đa thức tử không chia hết cho đa thức mẫu. Do đó, loại đáp án B.
Đồ thị hàm số trong hình 1.38 đi qua điểm \[\left( { - 2; - 3} \right)\]. Do đó, loại đáp án C.
Đồ thị hàm số trong hình 1.38 đi qua điểm (0; 1). Do đó, loại đáp án A.
Hàm số \(y = \frac{{{x^2} + x + 1}}{{x + 1}} = x + \frac{1}{{x + 1}}\) có:
+ \(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{{x^2} + x + 1}}{{x + 1}} = + \infty ;\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{{x^2} + x + 1}}{{x + 1}} = - \infty \) nên đường thẳng \(x = - 1\) là tiệm cận đứng của đồ thị hàm số.
+ \(\mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {x + \frac{1}{{x + 1}} - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 1}} = 0\), \(\mathop {\lim }\limits_{x \to - \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {x + \frac{1}{{x + 1}} - x} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x + 1}} = 0\) nên đường thẳng \(y = x\) là tiệm cận xiên của đồ thị hàm số.
Chọn D