Câu hỏi/bài tập:
Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n’} = \left( {A’;B’;C’} \right)\). Lấy các đường thẳng \(\Delta \), \(\Delta ‘\) tương ứng có vectơ chỉ phương \(\overrightarrow n ,\overrightarrow {n’} \) (H.5.36)
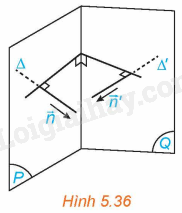
a) Góc giữa hai mặt phẳng (P) và (Q) và góc giữa hai đường thẳng \(\Delta \) và \(\Delta ‘\) có mối quan hệ gì?
b) Tính côsin của góc giữa hai mặt phẳng (P) và (Q).

Advertisements (Quảng cáo)
Sử dụng kiến thức về góc giữa hai mặt phẳng để tìm mối quan hệ: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta ‘\) tương ứng có vectơ chỉ phương \(\overrightarrow u ,\overrightarrow {u’} \) thì \(\cos \left( {\Delta ,\Delta ‘} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u’} } \right)} \right|\).

a) Vì các đường thẳng \(\Delta \), \(\Delta ‘\) tương ứng có vectơ chỉ phương \(\overrightarrow n ,\overrightarrow {n’} \) nên đường thẳng \(\Delta \) vuông góc với mặt phẳng (P), đường thẳng \(\Delta ‘\) vuông góc với mặt phẳng (Q).
Do đó, \(\left( {\left( P \right),\left( Q \right)} \right) = \left( {\Delta ,\Delta ‘} \right)\)
b) Ta có: \(\cos \left( {\Delta ,\Delta ‘} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n’} } \right)} \right|\) nên \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \cos \left( {\Delta ,\Delta ‘} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n’} } \right)} \right|\).
