Câu hỏi/bài tập:
(H.5.8) Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) không đi qua gốc tọa độ và cắt ba trục Ox, Oy, Oz tương ứng tại các điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) \(\left( {a,b,c \ne 0} \right)\).
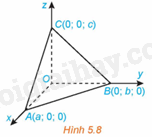
Chứng minh rằng mặt phẳng \(\left( \alpha \right)\) có phương trình \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) (Phương trình trên được gọi là phương trình mặt phẳng theo đoạn chắn).

Sử dụng kiến thức về lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng để viết: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau:
+ Tìm cặp vectơ chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \)
Advertisements (Quảng cáo)
+ Tìm vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
+ Lập phương trình tổng quát của mặt phẳng đi qua A và biết vectơ pháp tuyến là \(\overrightarrow n \).

Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - a;b;0} \right),\overrightarrow {AC} \left( { - a;0;c} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
Ta có: \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}b&0\\0&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - a}\\c&{ - a}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - a}&b\\{ - a}&0\end{array}} \right|} \right) = \left( {bc;ac;ab} \right)\)
Mặt phẳng (ABC) đi qua điểm A(a; 0; 0) và vectơ pháp tuyến \(\overrightarrow n = \left( {bc;ac;ab} \right)\) nên phương trình mặt phẳng (ABC) là:
\(bc\left( {x - a} \right) + acy + abz = 0 \Leftrightarrow bcx + acy + abz = bca \Leftrightarrow \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) (đpcm)
