Câu hỏi/bài tập:
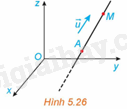
Trong không gian Oxyz, một vật thể chuyển động với vectơ vận tốc không đổi \(\overrightarrow u = \left( {a;b;c} \right) \ne \overrightarrow 0 \) và xuất phát từ điểm \(A\left( {{x_0};{y_0};{z_0}} \right)\) (H.5.26).
a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm mà nó đi qua và vectơ chỉ phương của đường thẳng đó)?
b) Giả sử tại thời điểm t \(\left( {t > 0} \right)\) tính từ khi xuất phát, vật thể ở vị trí \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right).\) Tính x, y, z theo a, b, c, \({x_0};{y_0};{z_0}\) và t.
Advertisements (Quảng cáo)

Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để xác định: Vectơ \(\overrightarrow u \ne \overrightarrow 0 \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).

a) Vật chuyển động trên đường thẳng qua A và song song với giá của vectơ \(\overrightarrow u \) (đi qua điểm A và vectơ chỉ phương của đường thẳng là \(\overrightarrow u \)).
b) Tại thời điểm t, vật ở vị trí \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) nên: \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\).
