Xét hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right) = \frac{1}{2}x\), trục hoành và hai đường thẳng \(x = 0, x = 4\)...

Xét hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right) = \frac{1}{2}x\), trục hoành và hai đường thẳng \(x = 0,x = 4\). Khi quay hình phẳng này xung quanh trục hoành Ox ta được khối nón có đỉnh là gốc O, trục là Ox và đáy là hình tròn bán kính bằng 2 (H.4.25).

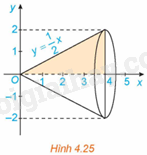
a) Tính thể tích V của khối nón.

b) Chứng minh rằng khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x \(\left( {0 \le x \le 4} \right)\) thì mặt cắt thu được là một hình tròn có bán kính là f(x), do đó diện tích mặt cắt là \(S\left( x \right) = \pi {f^2}\left( x \right)\). Tính \(\pi \int\limits_0^4 {{f^2}\left( x \right)dx} \) và so sánh với V.

Sử dụng kiến thức về thể tích khối nón để tính: Thể tích của khối nón có bán kính R, chiều cao h là: \(V = \frac{1}{3}\pi {R^2}h\).

a) Thể tích của khối nón là: \(V = \frac{1}{3}.\pi {.2^2}.4 = \frac{{16\pi }}{3}\)

b)

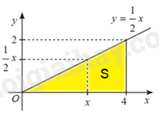
Khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x \(\left( {0 \le x \le 4} \right)\) thì mặt cắt thu được là một hình tròn có bán kính là \(f\left( x \right) = \frac{1}{2}x\).

Diện tích mặt cắt là: \(S\left( x \right) = \pi {f^2}\left( x \right) = \frac{1}{4}\pi {x^2}\).

Ta có: \(\pi \int\limits_0^4 {{f^2}\left( x \right)dx} = \pi \int\limits_0^4 {\frac{1}{4}{x^2}dx = \frac{{\pi {x^3}}}{{12}}\left| \begin{array}{l}4\\0\end{array} \right. = } \frac{{16\pi }}{3}\). Do đó, \(V = \pi \int\limits_0^4 {{f^2}\left( x \right)dx} \).