Câu hỏi/bài tập:
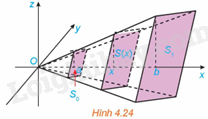
Tính thể tích của khối chóp cụt đều có diện tích hai đáy là \({S_o},{S_1}\) và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.

Sử dụng kiến thức về công thức tính thể tích vật để để tính: Cho một vật thể trong không gian Oxyz. Gọi \(\beta \) là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ \(x = a,x = b\). Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x cắt vật thể theo mặt cắt có diện tích là S(x). Giả sử S(x) là hàm số liên tục trên đoạn [a; b]. Khi đó thể tích V của phần vật thể \(\beta \) được tính bởi công thức \(V = \int\limits_a^b {S\left( x \right)dx} \).

Trong hệ trục tọa độ Oxyz, ta đặt khối chóp (tạo ra khối chóp cụt) sao cho đường cao nằm trên trục Ox và đỉnh trùng với gốc tọa độ.
Advertisements (Quảng cáo)
Gọi a và b lần lượt là khoảng cách từ O đến đáy nhỏ và đáy lớn. Khi đó, chiều cao của khối chóp cụt là: \(h = b - a\).
Thiết diện của khối chóp cụt đều cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \(\left( {a \le x \le b} \right)\) là một đa giác đều đồng dạng với đáy lớn với tỉ số đồng dạng là \(\frac{x}{b}\).
Ta có: \(\frac{{S\left( x \right)}}{{{S_1}}} = \frac{{{x^2}}}{{{b^2}}}\) nên \(S\left( x \right) = {S_1}.\frac{{{x^2}}}{{{b^2}}}\).
Thể tích của khối chóp cụt đều là:
\(V = \int\limits_a^b {{S_1}\frac{{{x^2}}}{{{b^2}}}dx} = \frac{{{S_1}\left( {{b^3} - {a^3}} \right)}}{{3{b^2}}} = \frac{{b - a}}{3}.\frac{{{S_1}{a^2} + {S_1}ab + {S_1}{b^2}}}{{{b^2}}} = \frac{h}{3}\left( {\frac{{{S_1}{a^2}}}{{{b^2}}} + \frac{{{S_1}a}}{b} + {S_1}} \right)\)
Lại có: \({S_0} = S\left( a \right) = \frac{{{S_1}{a^2}}}{{{b^2}}},\frac{{{S_1}a}}{b} = \sqrt {{S_1}.\frac{{{S_1}{a^2}}}{{{b^2}}}} = \sqrt {{S_1}{S_0}} \). Do đó, \(V = \frac{h}{3}\left( {{S_0} + \sqrt {{S_0}{S_1}} + {S_1}} \right)\)
Khối chóp đều được coi là khối chóp cụt đều có \({S_0} = 0\). Do đó, thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h là: \(V = \frac{1}{3}S.h\).
