Bài 21. Cho tam giác \(ABC\) vuông tại \(A, AB = c, AB = b\). Tính thể tích của khối tròn xoay sinh bởi tam giác đó (kể cả các điểm trong) khi quay quanh đường thẳng \(BC\).

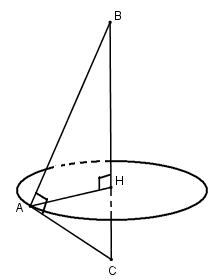
Gọi \(AH\) là đường cao của tam giác \(ABC\).
Ta có: \({1 \over {A{H^2}}} = {1 \over {A{B^2}}} + {1 \over {A{C^2}}} = {1 \over {{b^2}}} + {1 \over {{c^2}}} \Rightarrow A{H^2} = {{{b^2}{c^2}} \over {{b^2} + {c^2}}}\)
Advertisements (Quảng cáo)
Hai tam giác \(ABH\) và \(ACH\) khi quay quanh \(BC\) lần lượt tạo thành hai khối nón \({H_1},{H_2}\) có thể tích lần lượt là
\({V_1} = {1 \over 3}\pi A{H^2}BH\,\,\,\,{V_2} = {1 \over 3}\pi A{H^2}CH\)
Thể tích của khối tròn xoay sinh bởi tam giác \(ABC\) khi quay quanh \(BC\) là:
\(\eqalign{
& V = {V_1} + {V_2} = {1 \over 3}\pi A{H^2}BH + {1 \over 3}\pi A{H^2}CH = {1 \over 3}\pi A{H^2}BC \cr
& \,\,\,\,\, = {1 \over 3}\pi {{{b^2}{c^2}} \over {{b^2} + {c^2}}}\sqrt {{b^2} + {c^2}} = {{\pi {b^2}{c^2}} \over {3\sqrt {{b^2} + {c^2}} }} \cr} \)
