Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O dến AB bằng a và \(\widehat {SAO}\) = 300, \(\widehat {SAB}\) = 600. Tính diện tích xung quanh hình nón.

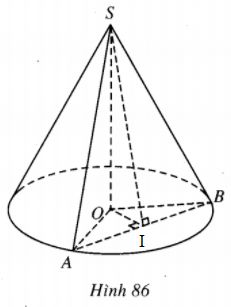
Gọi \(I\) là trung điểm của AB thì \(OI \bot AB,SI \bot AB,OI = a.\) Ta có
\(AO = SA\cos \) \(\widehat {SAO} ={{\sqrt 3 } \over 2}SA.\)
\(AI = SA\cos \) \(\widehat {SAI} ={1 \over 2}SA.\)
Advertisements (Quảng cáo)
Từ đó \({{AI} \over {AO}} = {1 \over {\sqrt 3 }}.\) Mặt khác \({{AI} \over {AO}} = \cos \widehat {IAO}\)
\( \Rightarrow \sin \widehat {IAO} ={{\sqrt 6 } \over 3} = {a \over {OA}}.\)
Vậy \(OA = {{3a} \over {\sqrt 6 }} = {{a\sqrt 6 } \over 2}.\)
Xét tam giác SAO, ta có \(SA = {{OA} \over {\cos {{30}^0}}} = {{a\sqrt 6 } \over 2}.{2 \over {\sqrt 3 }} = a\sqrt 2 .\)
Từ đó diện tích xung quanh của hình nón đã cho là
\({S_{xq}} = \pi .OA.SA = \pi .{{a\sqrt 6 } \over 2}.a\sqrt 2 = \pi {a^2}\sqrt 3 .\)
