Cho parabol (P): y = x2 và điểm A (-3;0). Xác định điểm M thuộc parabol (P) sao cho khoảng cách AM là ngắn nhất và tìm khoảng cách ngắn nhất đó.. Bài 24 trang 23 sách Đại số và Giải tích 12 Nâng cao - Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài 24. Cho parabol \((P): y = x^2\) và điểm \(A (-3;0)\). Xác định điểm \(M\) thuộc parabol \((P)\) sao cho khoảng cách \(AM\) là ngắn nhất và tìm khoảng cách ngắn nhất đó.
Gọi \(M\left( {x;{x^2}} \right)\)
Ta có: \(A{M^2} = {(x + 3)^2} + {x^4} = {x^4} + {x^2} + 6x + 9\)
\(AM\) đạt giá trị nhỏ nhất khi và chỉ khi \(f(x) = {x^4} + {x^2} + 6x + 9\) đạt giá trị nhỏ nhất
Advertisements (Quảng cáo)
Ta có: \(f'(x) = 4{x^3} + 2x + 6 = 2(x + 1)(2{x^2} - 2x + 3)\)
\(f’\left( x \right) = 0 \Leftrightarrow x = - 1;f\left( { - 1} \right) = 5\)
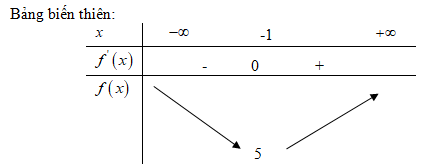
\(f\) đạt giá trị nhỏ nhất tại điểm \(x = -1\), giá trị nhỏ nhất là \(f (-1) = 5\).
\(AM\) đạt giá trị nhỏ nhất khi \(M\) ở vị trí \({M_0} (-1; 1)\) khi đó \(AM_0=\sqrt 5\)