b) Tùy theo các giá trị của m, hãy biện luận số nghiệm của phương trình: Bài 45 trang 44 SGK giải tích 12 nâng cao - Bài 6. Khảo sát sự biến thiên và vẽ đồ thị của một hàm số đa thức
Bài 45
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = {x^3} - 3{x^2} + 1\).
b) Tùy theo các giá trị của \(m\), hãy biện luận số nghiệm của phương trình: \({x^3} - 3{x^2} + m + 2 = 0\)

a) TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr
& y’ = 3{x^2} - 6x = 3x\left( {x - 2} \right);\,\,y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0;\,\,\,\,y\left( 0 \right) = 1 \hfill \cr
x = 2;\,\,\,\,y\left( 2 \right) = - 3 \hfill \cr} \right. \cr} \)
Bảng biến thiên:
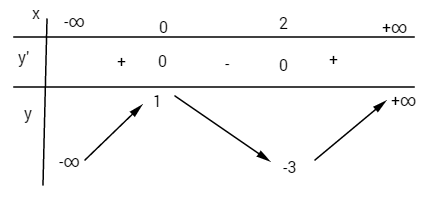
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\); nghịch biến trên khoảng \((0;2)\).
Hàm số đạt cực đại tại điểm \(x = 0\), giá trị cực đại \(y(0) = 1\); hàm số đat cực tiểu tại điểm \(x = 2\), giá trị cực tiểu \(y(2) = -3\).
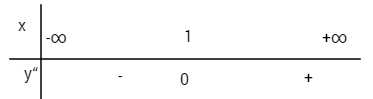
\(y” = 6x - 6;\,y” = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = - 1\)
Xét dấu \(y”\)
Advertisements (Quảng cáo)
Điểm uốn của đồ thị \(I(1;-1)\)
Điểm đặc biệt \(x = - 1 \Rightarrow y = - 3\)
Đồ thị: đồ thị nhận điểm \(I(1;-1)\) làm tâm đối xứng.
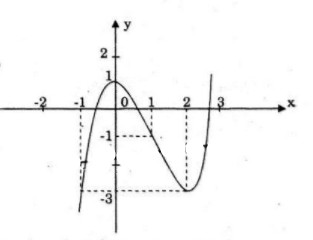
b) Ta có: \({x^3} - 3{x^2} + m + 2 = 0 \Leftrightarrow {x^3} - 3{x^2} + 1 = - m - 1\)
Số nghiệm của phương trình trên bằng số giao điểm của đồ thị hàm số \(y = {x^3} - 3{x^2} + 1\) và
đường thẳng \(y = - m -1\). Dựa vào đồ thị ta có:
- Nếu \( - m - 1<-3\Rightarrow m>2\) thì phương trình có \(1\) nghiệm.
- Nếu \(-m-1=-3\Rightarrow m=2\) thì phương trình có \(2\) nghiệm.
- Nếu \(-3< -m-1<1\Rightarrow -2<m<2\) thì phương trình có \(3\) nghiệm.
- Nếu \(-m-1=1\Rightarrow m=-2\) thì phương trình có \(2\) nghiệm
- Nếu \(-m-1>1\Rightarrow m<-2\) thì phương trình có \(1\) nghiệm.
