a) Tìm các giá trị của m sao cho hàm số có ba cực trị.
b) Kháo sát sự biến thiên và vẽ đồ thị của hàm số với . Viết phương trình tiếp tuyến của đồ thị tại hai điểm uốn.
. Bài 48 trang 45 SGK giải tích 12 nâng cao - Bài 6. Khảo sát sự biến thiên và vẽ đồ thị của một hàm số đa thức
Bài 48. Cho hàm số: \(y = {x^4} - 2m{x^2} + 2m\)
a) Tìm các giá trị của \(m\) sao cho hàm số có ba cực trị.
b) Kháo sát sự biến thiên và vẽ đồ thị của hàm số với \(m = {1 \over 2}\). Viết phương trình tiếp tuyến của đồ thị tại hai điểm uốn.

a) TXĐ: \(D =\mathbb R\)
\(y = 4{x^3} - 4mx = 4x\left( {{x^2} - m} \right);\,y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
{x^2} = m \hfill \cr} \right.\)
Nếu \(m> 0\) thì \(y’=0\) \( \Leftrightarrow x = 0\) hoặc \(x = - \sqrt m \) hoặc \(x = \sqrt m \)
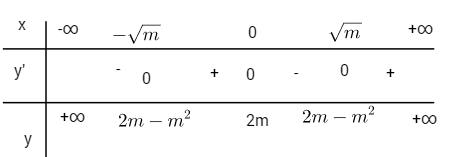
Hàm số có ba điểm cực trị.
Nếu \(m \le 0\) thì \({x^2} - m \ge 0\) với mọi \(x \in\mathbb R\)
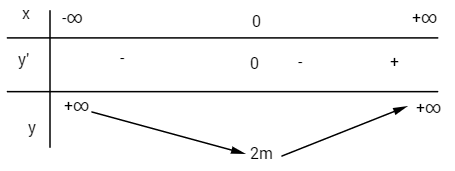
Hàm số có \(1\) cực tiểu.
Vậy hàm số có ba cực trị khi và chỉ khi \(m>0\).
b) Với \(m = {1 \over 2}\) ta có \(y = {x^4} - {x^2} + 1\)
TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \cr
& y’ = 4{x^3} - 2x = 2x\left( {2{x^2} - 1} \right);\,y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0;\,\,\,\,y\left( 0 \right) = 1 \hfill \cr
x = \pm \sqrt {{1 \over 2}} ;\,\,y\left( { \pm \sqrt {{1 \over 2}} } \right) = {3 \over 4} \hfill \cr} \right. \cr} \)
Advertisements (Quảng cáo)
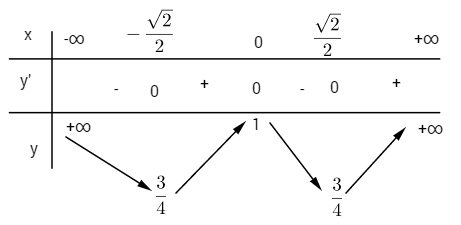
\(y” = 12{x^2} - 2;\,y” = 0 \Leftrightarrow x = \pm {{\sqrt 6 } \over 6};\,\,y\left( { \pm {{\sqrt 6 } \over 6}} \right) = {{31} \over {36}}\)
Xét dấu y”
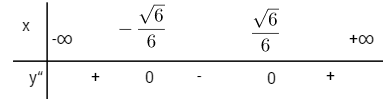
Đồ thị có hai điểm uốn: \({I_1}\left( { - {{\sqrt 6 } \over 6};{{31} \over {36}}} \right)\) và \({I_2}\left( {{{\sqrt 6 } \over 6};{{31} \over {36}}} \right)\)
Điểm đặc biệt: \(x = \pm 1 \Rightarrow y = 1\)
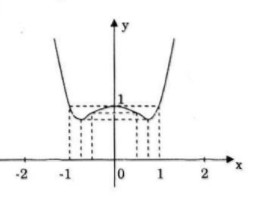
Đồ thị: Đồ thị nhận trục tung làm trục đối xứng.
+ Phương trình tiếp tuyến tại \({I_1}\left( { - {{\sqrt 6 } \over 6};{{31} \over {36}}} \right)\) là \(y - {{31} \over {36}} = y’\left( { - {{\sqrt 6 } \over 6}} \right)\left( {x + {{\sqrt 6 } \over 6}} \right)\)
\( \Leftrightarrow y = {4 \over {3\sqrt 6 }}x + {{13} \over {12}}\)
+ Tương tự phương trình tiếp tuyến tại \({I_2}\left( {{{\sqrt 6 } \over 6};{{31} \over {36}}} \right)\) là: \(y = - {4 \over {3\sqrt 6 }}x + {{13} \over {12}}\)
