Bài 40
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số
\(y = {x^3} + 3{x^2} - 4\)
b) Viết phương trình tiếp tuyến của đồ thị tại điểm uốn.
c) Chứng minh rằng điểm uốn là tâm đối xứng của đồ thị.

a) Tập xác đinh: \(D=\mathbb R\)
Sự biến thiên:
\(\eqalign{
& y’ = 3{x^2} + 6x \cr
& y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = - 2 \hfill \cr} \right. \cr} \)
- Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {0; + \infty } \right)\)
- Hàm số nghịch biến trên khoảng \((-2;0)\)
- Cực trị:
Hàm số đạt cực đại tại \(x=-2\;;y_{CĐ}=0\)
Hàm số đạt cực tiểu tại \(x=0\;;y_{CT}=-4\)
- Giới hạn:
Advertisements (Quảng cáo)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} + 3{x^2} - 4} \right) = + \infty \cr
& \mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} + 3{x^2} - 4} \right) = - \infty \cr} \)
\(\eqalign{
& y” = 6x + 6 \cr
& y” = 0 \Leftrightarrow x = - 1 \cr} \)
Điểm uốn \(I(-1;-2)\)
- Bảng biến thiên:
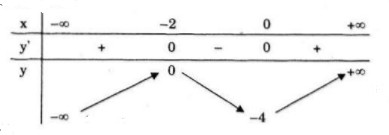
Đồ thị:
Đồ thị hàm số nhận điiểm \(I(-1;-2)\) làm tâm đối xứng.
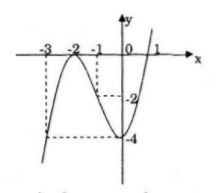
b) \(y'(-1)=-3\)
Phương trình tiếp tuyến với đồ thị tại \(I(-1;-2)\) là:
\(y=-3(x+1)+(-2) \Leftrightarrow y = - 3x - 5\)
c) Đồ thị nhận \(I(-1;-2)\) làm tâm đối xứng khi và chỉ khi:
\(\eqalign{
& y\left( { - 1 + x} \right) + y\left( { - 1 - x} \right) = 2.\left( { - 2} \right) \cr
& \Leftrightarrow {\left( { - 1 + x} \right)^3} + 3{\left( { - 1 + x} \right)^2} - 4 + {\left( { - 1 - x} \right)^3} + 3{\left( { - 1 - x} \right)^2} - 4 = - 4 \cr
& \Leftrightarrow - 1 + 3x - 3{x^2} + {x^3} + 3 - 6x + 3{x^2} - 4 - 1 - 3x - 3{x^2} - {x^3} + 3 + 6x + 3{x^2} - 4 = - 4 \cr
& \Leftrightarrow - 4 = - 4\,\,\forall x \cr} \)
\(\Leftrightarrow I(-1;-2)\) là tâm đối xứng của đồ thị.
