Cho hình phẳng A được giới hạn bởi đường cong có phương trình và các đường thẳng Tính thể tích khối tròn xoay tạo được khi quay A. Bài 59 Trang 177 SGK Đại số và Giải tích 12 Nâng cao - Ôn tập chương III - Nguyên hàm tích phân và ứng dụng
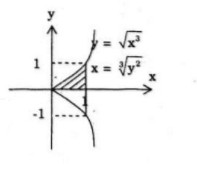
Bài 59. Cho hình phẳng A được giới hạn bởi đường cong có phương trình \({y^2} = {x^3}\) và các đường thẳng \(y = 0,x = 1.\) Tính thể tích khối tròn xoay tạo được khi quay A
a) Quanh trục hoành; b) Quanh trục tung.
Advertisements (Quảng cáo)
a) Ta có \(y = \sqrt {{x^3}} \,\,\left( {y \ge 0} \right)\)
Thể tích cần tìm là: \(V = \pi \int\limits_0^1 {{x^3}dx = \left. {{{\pi {x^4}} \over 4}} \right|} _0^1 = {\pi \over 4}\)
b) Ta có \(x = \root 3 \of {{y^2}} \)
Thể tích cần tìm là: \(V = \pi \int\limits_0^1 {\left( {{1^2}-\root 3 \of {{y^4}} } \right)} dy = \left. {\pi \left( {y - {3 \over 7}{y^{{7 \over 3}}}} \right)} \right|_0^1 = {{4\pi } \over 7}.\)