Tính diện tích hình phẳng giới hạn bởi:
a) Đồ thị hai hàm số \(y = \left| {{x^2} - 4} \right|,y = {{{x^2}} \over 2} + 4\)
b) Các đường cong \(x = {y^{{2 \over 3}}},x + {y^4} = 2\) và trục hoành.
c) Các đường cong \(y = \sqrt x ,x + 2{y^2} = 3\) và trục hoành.
Giải
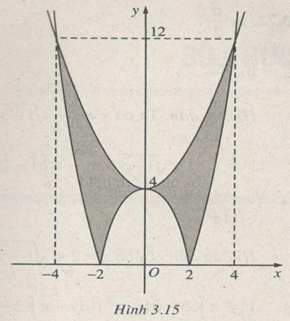
a) (h.3.15)
\(S = 2\int\limits_0^4 {\left( {{{{x^2}} \over 2} + 4 - \left| {{x^2} - 4} \right|} \right)} dx\)
Advertisements (Quảng cáo)
\(= 2\int\limits_0^2 {\left[ {{{{x^2}} \over 2} + 4 - \left( {4 - {x^2}} \right)} \right]} dx \)
\(+ 2\int\limits_2^4 {\left[ {{{{x^2}} \over 2} + 4 - ({{x^2} - 4} )} \right]} dx = {{64} \over 3}\)
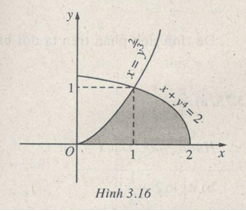
b) (h.3.16)
\(S = \int\limits_0^1 {{x^{{3 \over 2}}}dx + } \int\limits_1^2 {{{\left( {2 - x} \right)}^{{1 \over 4}}}} dx = {2 \over 5} + {4 \over 5} = {6 \over 5}\)
c) \(S = \int\limits_0^1 {\sqrt x dx + \int\limits_1^3 {\sqrt {{{3 - x} \over 2}} } } dx = {2 \over 3} + {4 \over 3} = 2\)
