Bài 11. Cho hình hộp \(ABCD.A’B’C’D’\). Gọi \(E\) và \(F\) theo thứ tự là trung điểm của các cạnh \(BB’\) và \(DD’\). Mặt phẳng \((CEF)\) chia khối hộp trên làm hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó.

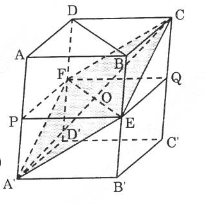
Ta xác định thiết diện của hình hộp \(ABCD.A’B’C’D’\) khi cắt bởi \((CEF)\). Mặt phẳng \((CEF)\) chứa đường thẳng \(EF\) mà \(E\) là trung điểm của \(BB’, F\) là trung điểm của \(CC’\) nên \(EF\) chứa giao điểm \(O\) của các đường chéo hình hộp, do đó mặt phẳng \((CEF)\) cùng chứa giao điểm \(O\) của các đường chéo và nó cũng chứa đường chéo \(A’C\) của hình hộp. Ta dễ dàng nhận xét rằng thiết diện chính là hình bình hành \(CEA’F\). Qua \(EF\) ta dựng một mặt phẳng song song với đáy hình hộp, mặt phẳng này cắt \(AA’\) ở \(P\) và cắt \(CC’\) ở \(Q\).
Ta có thể tích của hình hộp \(ABCD.PEQF\) là:
\(V_{ABCD.PEQF}\)= \({1 \over 2}\)\(V_{ABCD.A’B’C’D’}\) (1)
Chứng minh tương tự ta được:
\(V_{CFQE}=V_{A’FPE}\) (2)
Advertisements (Quảng cáo)
(Hai hình chóp \(CFQE\) và \(A’FPE\) có chiều cao bằng nhau và diện tích đáy bằng nhau).
Xét khối đa diện \(ABCDE’F\) do mặt phẳng \((CEF)\) chia ra trên hình hộp \(ABCD.A’B’C’D’\), ta có:
\(V_{ABCD.FA’EQ}\) = \({1 \over 2}\) \(V_{ABCD.FPE}+V_{A’FPE}\) (3)
Từ (1), (2), (3) suy ra:
\(V_{ABCD.FA’EQ}\)= \({1 \over 2}\) \(V_{ABCD.A’B’C’D’}\)
Vậy mặt phẳng \((CEF)\) chia hình hộp thành hai khối đa diện có thể tích bằng nhau, tỉ số của chúng là \(1\).
Chú ý: Có thể lí luận như sau: Giao điểm \(O\) của các đường chéo của hình hộp là tâm đối xứng của hình hộp, do đó mặt phẳng \((CEF)\) chứa điểm \(O\) nên chia hình hộp thành hai hình đối xứng với nhau qua điểm \(O\). Vậy hai hình này là hai hình bằng nhau và có thể tích bằng nhau.
