Bài 5 trang 26 SGK Hình học 12: Ôn tập chương I - Khối đa diện. Cho hình chóp tam giác O.ABC
Bài 5. Cho hình chóp tam giác \(O.ABC\) có ba cạnh \(OA, OB, OC\) đôi một vuông góc với nhau và \(OA = a, OB = b, OC = c\). Hãy tính đường cao \(OH\) của hình chóp.
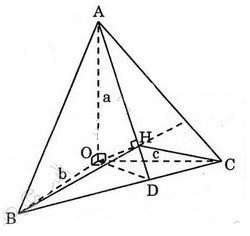
Kẻ \(AD\bot BC, OH \bot AD\) thì dễ thấy \(OH\) chính là đường cao của hình chóp.
Advertisements (Quảng cáo)
Vì \(OD.BC = OB.OC\) nên \(OD ={{bc} \over {\sqrt {{b^2} + {c^2}} }}\) . Từ đó suy ra
\(AD = \sqrt {{a^2} + {{{b^2}{c^2}} \over {{b^2} + {c^2}}}}\) = \(\sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}}\) .
Vì \(OH.AD = OA.OD\) nên
\(OH = {{abc} \over {\sqrt {{b^2} + {c^2}} }}:\sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}} = {{abc} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)