Bài 6. Cho hình chóp tam giác \(S.ABC\) có cạnh \(AB\) bằng \(a\). Các cạnh bên \(SA, SB, SC\) tạo với đáy một góc \(60^0\). Gọi \(D\) là giao điểm của \(SA\) với mặt phẳng qua \(BC\) và vuông góc với \(SA\).
a) Tính tỉ số thể tích của hai khối chóp \(S.DBC\) và \(S.ABC\).
b) Tính thể tích của khối chóp \(S.DBC\).

a) Vì hình chóp \(S.ABC\) là hình chóp đều nên chân đường cao \(H\) là tâm của đường tròn ngoại tiếp đáy, theo giả thiết, ta có: góc \(SAH = 60^0\). Gọi \(M\) là trung điểm của cạnh \(BC\) thì \(AM\) là đường cao của tam giác đều \(ABC\):
\(AM = {{a\sqrt 3 } \over 2}\)
\(AH = {2 \over 3}.AM = {{a\sqrt 3 } \over 3}\)
Từ đây, ta có:\(SA = {{AH} \over {c{\rm{os}}{{60}^0}}}\) = \({{2a\sqrt 3 } \over 3}\)
\(AD = AM.cos 60^0\) = \({{a\sqrt 3 } \over 4}\)
Advertisements (Quảng cáo)
\(\Rightarrow SD = SA - AD = {{5a\sqrt 3 } \over {12}}\)
Áp dụng công thức tỉ số thể tích trong bài tập 4, 3 (trang 37 SGK) ta được:
\({{{V_{S.DBC}}} \over {{V_{S.ABC}}}} = {{SD} \over {SA}}.{{SB} \over {SB}}.{{SC} \over {SC}} = {{5a\sqrt 3 } \over {12}}:{{2a\sqrt 3 } \over 3} = {5 \over 8}\)
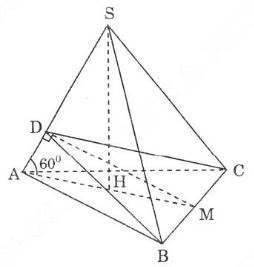
b) Ta có: \(S_{ABC}\) = \({{{a^2}\sqrt 3 } \over 4}\); \(SH = AH.tan60^0 = a\)
\( \Rightarrow {V_{S.ABC}} = {1 \over 3}.SH.{S_{ABC}}\) \( \Rightarrow {V_{S.ABC}} = {{{a^3}\sqrt 3 } \over {12}}\)
Từ kết quả câu a) ta có:
\({V_{S.DBC}} = {5 \over 8}.{V_{S.ABC}}\) \( \Rightarrow {V_{S.BDC}} = {5 \over 8}.{{{a^3}\sqrt 3 } \over {12}}\)
\( \Rightarrow {V_{S.DBC}} = {{5{a^3}\sqrt 3 } \over {96}}\)
