Bài 1. Tính diện tích hình phẳng giới hạn bởi các đường:
a) \(y={x^2},y =x + 2\);
b) \(y = |lnx|, y = 1\);
c) \(y = {\left( x-6 \right)}^2,y = 6x-{x^2}\)
Hướng dẫn giải :
a) Phương trình hoành độ giao điểm \(f(x) = x^2-x -2 =0 ⇔ x = -1\) hoặc \(x = 2\).
Diện tích hình phẳng cần tìm là :
\(S=\int_{-1}^{2}\left |x^{2}- x- 2 \right |dx = \left | \int_{-1}^{2}\left (x^{2}- x- 2 \right ) dx \right |\)
\(=\left |\frac{x^{3}}{3}-\frac{x^{2}}{2}-2x|_{-1}^{2} \right |=\left |\frac{8}{3}-2-4-(\frac{1}{3}-\frac{1}{2}+2) \right |\)\(=4\tfrac{1}{2}\)
b) Phương trình hoành độ giao điểm:
\(f(x) = 1 - ln|x| = 0 ⇔ lnx = ± 1\)
\(⇔ x = e\) hoặc \(x = \frac{1}{e}\) 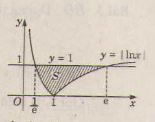
\(y = ln|x| = lnx\) nếu \(lnx ≥ 0\) tức là \(x ≥ 1\).
hoặc \(y = ln|x| = - lnx\) nếu \(lnx < 0\), tức là \(0 < x < 1\).
Advertisements (Quảng cáo)
Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :
\(S=\int_{\frac{1}{e}}^{e}|1- ln|x||dx =\int_{\frac{1}{e}}^{1}(1+lnx)dx \)
\(+\int_{1}^{e}(1-lnx)dx\)
\(= x|_{\frac{1}{e}}^{1}+\int_{\frac{1}{e}}^{1}lnxdx +x|_{1}^{e}-\int_{1}^{e}lnxdx\)
\(=-\frac{1}{e}+e+\int_{\frac{1}{e}}^{1}lndx-\int_{1}^{e}lnxdx\)
Ta có \(∫lnxdx = xlnx - ∫dx = xlnx – x + C\), thay vào trên ta được :
\(S=e-\frac{1}{e}+(xlnx-x)|_{\frac{1}{e}}^{1}- (xlnx-x)|_{1}^{e}\)\(=e+\frac{1}{e}-2\)
c) Phương trình hoành độ giao điểm là:
\(f\left( x \right) =6x-{x^2}-{\left( {x -6} \right)^2} = - 2({x^2}-9x+ 18)\)\(=0\)
\(⇔ - 2({x^2}-9x+ 18) ⇔ x = 3\) hoặc \(x = 6\).
Diện tích cần tìm là:
\(S=\int_{3}^{6}|-2(x^{2}-9x+18)|dx\)
\(=|2\int_{3}^{6}(x^{2}-9x+18)dx|\)
\(=\left |2(\frac{x^{3}}{3}-\frac{9}{2}x^{2}+18x)|_{3}^{6} \right |=9\).
