a) Vẽ góc bẹt xOy.
b) Vẽ tia Ot sao cho \(\widehat {xOt} = {30^o}\)
c) Vẽ tia Oz sao cho \(\widehat {y{\rm{O}}z} = {30^o}\) (Ot và Oz cùng nằm trên một nửa mặt phẳng bờ xy)
d) Vẽ tia phân giác Om của góc tOz;
e) Vì sao tia Om cũng là tia phân giác của \(\widehat {xOy}\)?
Giải
a) Ta có hình vẽ các câu a, b, c, d.
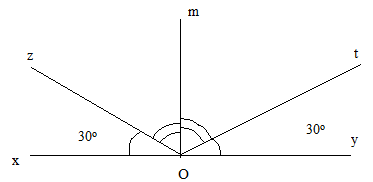
e) Vì \(\widehat {xOt}\) và \(\widehat {tOy}\) kề bù nên: \(\widehat {xOt} + \widehat {tOy} = {180^o}\)
Thay \(\widehat {xOt} = {30^o}\) ta có:
Advertisements (Quảng cáo)
\({30^o} + \widehat {tOy} = {180^o}\)
\( \Rightarrow \widehat {tOy} = {180^o} - {30^o} = {150^o}\)
Vì Oz và Ot nằm trên nửa mặt phẳng bờ chứa tia Oy
\(\widehat {xOz} < \widehat {y{\rm{O}}t}\) nên tia Oz nằm giữa tia Oy và Ot
\( \Rightarrow \widehat {y{\rm{O}}z} + \widehat {zOt} = \widehat {y{\rm{O}}t}\)
\({30^o} + \widehat {zOt} = {150^o}\)
\( \Rightarrow \widehat {zOt} = {150^o} - {30^o} = {120^o}\)
Vì tia Om là tia phân giác \(\widehat {tOz}\) nên \(\widehat {tOm} = \widehat {mOz} = {{\widehat {tOz}} \over 2} = {60^o}\)
Vì Ot nằm giữa Ox và Om nên \(\widehat {xOt} + \widehat {tOm} = \widehat {xOm}\)
\( \Rightarrow \widehat {xOm} = {30^o} + {60^o} = {90^o}\). Vậy Om là tia phân giác \(\widehat {xOy}\).
