
Cho ba tia phân biệt Oa, Ob, Oc. Biết rằng \(\widehat {aOb} = {45^o},\widehat {bOc} = {135^o}\) và tia Ob nằm giữa hai tia Oa, Oc. Vẽ tia Om là phân giác của góc aOb và tia On là phân giác của góc bOc. Hãy tính số đo của góc mOn.

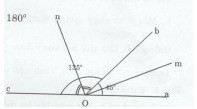
Tia Ob nằm giữa hai tia On và Oc.
Nên \(\widehat {aOb} + \widehat {bOc} = \widehat {aOc}\)
\(\Rightarrow \widehat {aOc} = {45^0} + {135^0} = {180^0}.\)
Advertisements (Quảng cáo)
Do đó: Oc và Oa là hai tia đối nhau.
Om là tia phân giác của góc aOb.
Nên \(\widehat {mOb} = {1 \over 2}\widehat {aOb}\) và On là tia phân giác của góc bOc nên \(\widehat {bOn} = {1 \over 2}\widehat {bOc}.\)
Tia Ob nằm giữa hai tia Om và On nên \(\widehat {mOn} = \widehat {mOb} + \widehat {bOn}\)
Do đó \(\widehat {mOn} = {1 \over 2}\widehat {aOb} + {1 \over 2}\widehat {bOc} \)\(\,= {1 \over 2}(\widehat {aOb} + \widehat {bOc}) = {1 \over 2}{.180^0} = {90^0}.\)
