
Cho tam giác ABC có \(\widehat {ABC} = 53^\circ ,\widehat {BAC} = 90^\circ \) , AH vuông góc với BC (H thuộc BC). Vẽ tia Bx vuông góc với BC. Trên tia Bx lấy điểm D sao cho BD = HA (Hình 23).
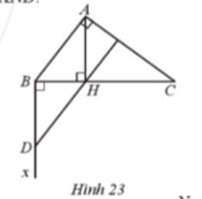
a) Chứng minh ∆AHB = ∆DBH.
b) Chứng minh DH vuông góc với AC.
c) Tính số đo góc BDH.

- Xét các điều kiện về cạnh và góc để chứng minh ∆AHB = ∆DBH
- Từ đó suy ra các góc tương ứng bằng nhau để chứng minh DH vuông góc với AC và tính số đo góc BDH.

a) Xét ∆AHB và ∆DBH có:
\(\widehat {AHB} = \widehat {HB{\rm{D}}}\) (cùng bằng 90°),
BH là cạnh chung,
Advertisements (Quảng cáo)
AH = BD (giả thiết),
Suy ra ∆AHB = ∆DBH (hai cạnh góc vuông).
Vậy ∆AHB = ∆DBH.
b) Do ∆AHB = ∆DBH (chứng minh câu a) nên \(\widehat {ABH} = \widehat {DHB}\) (hai góc tương ứng).
Mà \(\widehat {ABH},\widehat {DHB}\) ở vị trí so le trong
Do đó AB // DH.
Lại có, AB ⊥ AC nên DH ⊥ AC (một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại).
Vậy DH ⊥ AC.
c) Do ∆AHB = ∆DBH (chứng minh câu a) nên\(\widehat {BAH} = \widehat {HDB}\) (hai góc tương ứng).
Xét tam giác ABH vuông tại H có:
\(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra \(\widehat {BAH} = 90^\circ - \widehat {ABH} = 90^\circ - 53^\circ = 37^\circ \).
Do đó \(\widehat {BDH} = 37^\circ \).
Vậy \(\widehat {BDH} = 37^\circ \)
