
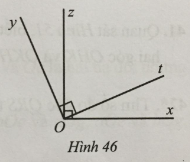
Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot.
a) Hai góc xOt và yOz có bằng nhau hay không?
b) Chứng tỏ \(\widehat {xOy} + \widehat {zOt} = 180^\circ \).
c) Vẽ tia Ou là tia phân giác của góc tOz. Tia Ou có phải là tia phân giác của góc xOy hay không?

a) Để xem hai góc có bằng nhau không, ta tính tổng số đo của hai góc đó với một góc trung gian khác.
b) Chứng minh tổng hai góc bằng 180° dựa vào hai góc kề nhau.
c) Muốn biết tia Ou có là phân giác của góc xOy hay không, ta tính số đo góc của các góc tạo bởi tia Ou, Ox và Oy.
Advertisements (Quảng cáo)

a) Ta có: các cặp góc xOt và zOt, yOt và zOt là các cặp góc kề nahu nên
\(\widehat {xOt} + \widehat {zOt} = \widehat {xOz} = 90^\circ ,{\rm{ }}\widehat {yOz} + \widehat {zOt} = \widehat {yOt} = 90^\circ \).
Do đó: \(\widehat {xOt} = \widehat {yOz}\).
b) Ta có hai góc yOz và xOz là hai góc kề nhau nên \(\widehat {yOz} + \widehat {xOz} = \widehat {xOy}\).
Suy ra: \(\begin{array}{l}\widehat {xOy} + \widehat {zOt} = \widehat {yOz} + \widehat {xOz} + \widehat {zOt}\\ = \widehat {xOz} + \left( {\widehat {yOz} + \widehat {zOt}} \right)\\ = \widehat {yOz} + \widehat {zOt}\\ = 90^\circ + 90^\circ = 180^\circ \end{array}\)
c)
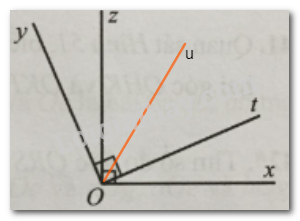
Do Ou là tia phân giác của góc tOz nên \(\widehat {tOu} = \widehat {zOu}\).
Ta có: các cặp góc tOu và xOt, zOu và yOz là các cặp góc kề nhau nên \(\widehat {tOu} + \widehat {xOt} = \widehat {xOu},{\rm{ }}\widehat {zOu} + \widehat {yOz} = \widehat {yOu}\).
Mà \(\widehat {tOu} = \widehat {zOu},{\rm{ }}\widehat {xOt} = \widehat {yOz} \Rightarrow \widehat {xOu} = \widehat {yOu}\).
Mà Ou nằm giữa hai tia Ox và Oy nên Ou là tia phân giác của góc xOy.
