
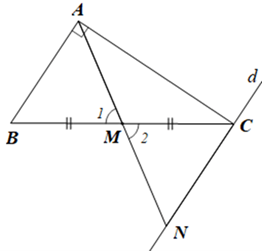
Cho tam giác ABC có \(\hat A = 90^\circ \), M là trung điểm của BC. Chứng minh BC = 2AM.

- Chứng minh \(\Delta MBA = \Delta MCN(g - c - g)\)
Suy ra: AB = CN và AM = MN
- Chứng minh: \(\Delta BAC = \Delta NCA\) từ đó chứng minh được BC = 2AM

Qua C kẻ đường thẳng d song song với AB, d cắt AM tại N.
Suy ra \(\widehat {ABC} = \widehat {BCN}\) (hai góc so le trong).
Ta có BA ⊥ AC, d // AB.
Suy ra d ⊥ AC hay \(\widehat {NCA} = 90^\circ \)
Advertisements (Quảng cáo)
Xét ∆MBA và ∆MCN có:
BM = CM (vì M là trung điểm của BC),
\({\hat M_1} = {\hat M_2}\) (hai góc đối đỉnh),
\(\widehat {ABC} = \widehat {NCB}\) (chứng minh trên)
Do đó ∆MBA = ∆MCN (g.c.g).
Suy ra AB = CN và AM = NM (các cặp cạnh tương ứng).
Xét ∆BAC và ∆NCA có:
AC là cạnh chung,
\(\widehat {BAC} = \widehat {NCA}\) (cùng bằng 90o),
AB = NC (chứng minh trên)
Do đó ∆BAC = ∆NCA (c.g.c)
Suy ra BC = NA (hai cạnh tương ứng).
Mà AM = MN, AN = AM + MN = 2AM.
Nên BC = AN = 2AM.
Vậy 2AM = BC.
