
Cho tam giác ABC vuông tại A có \(\hat C = 30^\circ \). Đường trung trực của BC cắt AC tại M. Chứng minh:
a) BM là tia phân giác của góc ABC;
b) MA < MC.

- Chứng minh: \(\widehat {{B_1}} = \widehat {{B_2}}\) suy ra BM là tia phân giác của góc ABC
- Chứng minh: MA < MB và MA = MC suy ra MA < MC

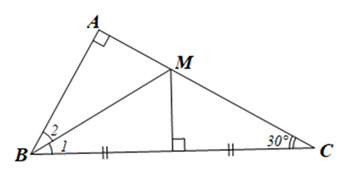
a) Vì DABC vuông tại A nên \(\widehat {ABC} + \hat C = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90o).
Suy ra \(\widehat {ABC} = 90^\circ - \hat C = 90^\circ - 30^\circ = 60^\circ \)
Advertisements (Quảng cáo)
Vì điểm M thuộc đường trung trực của BC nên MB = MC.
Do đó tam giác MBC cân ở M.
Suy ra \({\hat B_1} = \hat C = 30^\circ \)
Mặt khác \({\hat B_1} + {\hat B_2} = \widehat {ABC} = 60^\circ \) (hai góc kề nhau)
Nên \({\hat B_2} = \widehat {ABC} - {\hat B_1} = 60^\circ - 30^\circ = 30^\circ \)
Suy ra \({\hat B_2} = {\hat B_1}\)
Do đó BM là tia phân giác của góc ABC.
Vậy BM là tia phân giác của góc ABC.
b) Trong tam giác vuông ABM có MA < MB (trong tam giác vuông, cạnh huyển là cạnh lớn nhất).
Mà MB = MC (chứng minh câu a).
Suy ra MA < MC.
Vậy MA < MC.
