
Cho góc xOy khác góc bẹt. Oz là tia phân giác của góc đó, M là một điểm bất kì thuộc tia Oz. Qua M vẽ đường thẳng a vuông góc với Ox tại A, cắt Oy tại C. Qua M vẽ đường thẳng b vuông góc với Oy tại B, cắt Ox tại D. Chứng minh:
a) OM là đường trung trực của đoạn thẳng AB;
b) Tam giác DMC là tam giác cân.

- Chứng minh: O và M cùng nằm trên đường trung trực của BC.
Suy ra: OM là đường trung trực của AB.
- Chứng minh: \(\Delta A{\rm{D}}M = \Delta BCM\) nên MD = MC
Suy ra tam giác DMC cân tại M.

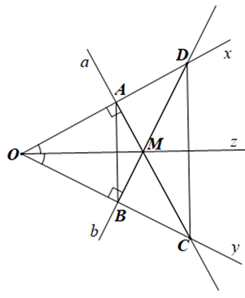
a) Vì Oz là tia phân giác của góc xOy nên \(\widehat {xOz} = \widehat {zOy}\)
Xét ∆OAM và ∆OBM có
Advertisements (Quảng cáo)
\(\widehat {OAM} = \widehat {OBM}\left( { = 90^\circ } \right)\)
OM là cạnh chung,
\(\widehat {AOM} = \widehat {BOM}\) (do \(\widehat {xOz} = \widehat {zOy}\))
Do đó ∆OAM = ∆OBM (cạnh huyền – góc nhọn).
Suy ra OA = OB và MA = MB (các cặp cạnh tương ứng).
Nên O và M cùng nằm trên đường trung trực của AB.
Vậy OM là đường trung trực của AB.
b) Xét ∆ADM và ∆BCM có
\(\widehat {DAM} = \widehat {CBM}\left( { = 90^\circ } \right)\),
AM = BM (chứng minh câu a),
\(\widehat {AMD} = \widehat {BMC}\) (hai góc đối đỉnh)
Do đó ∆ADM = ∆BCM (cạnh huyền – góc nhọn).
Suy ra MD = MC (hai cạnh tương ứng).
Do đó tam giác CDM cân tại M.
Vậy tam giác DMC cân tại M.
