
Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng \(\widehat {BAC} = 90^\circ \)

- Chứng minh hai tam giác AMD và AMC cân tại M.
- Tổng ba góc của một tam giác bằng \({180^o}\).
Từ đó chứng minh \(\widehat {BAC} = {90^o}\)

Advertisements (Quảng cáo)
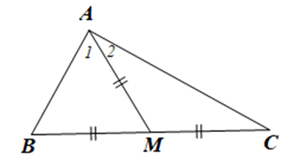
Ta có: \(AM = \frac{1}{2}BC, BM = MC\) nên \(AM = BM = MC\).
Suy ra hai tam giác AMB và AMC cân tại M.
Do đó \(\widehat B = {\hat A_1},\hat C = {\hat A_2}\)
Xét \(\Delta ABC\) có \(\widehat B + \widehat C + \widehat {BAC} = 180^\circ \) (tổng ba góc của một tam giác)
Suy ra \({\widehat A_1} + {\widehat A_2} + \widehat {BAC} = 180^\circ \) hay \(\widehat {BAC} + \widehat {BAC} = 180^\circ \)
Nên \(2\widehat {BAC}= 180^\circ \)
Do đó \(\widehat {BAC} = \frac{{180^\circ }}{2} = 90^\circ \)
Vậy \(\widehat {BAC} = 90^\circ \)
