
Cho hai tam giác đều chung đáy ABC và BCD. Gọi I là trung điểm của BC. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Đường thẳng BC là đường trung trực của AD.
b) Điểm I cách đều các điểm A, B, D.
c) Điểm B nằm trên đường trung trực của CD.
d) Điểm C không nằm trên đường trung trực của BD.

Sử dụng tính chất ba đường trung trực của tam giác để xác định các phát biểu đúng sai

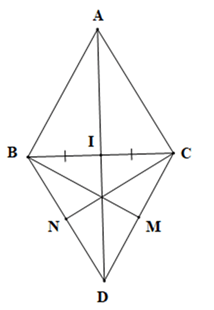
Vì tam giác ABC, DBC là tam giác đều nên AB = AC = BC = BD = DC.
•Ta có CA = CD nên C nằm trên đường trung trực của đoạn thẳng AD.
Advertisements (Quảng cáo)
Do BA = BD nên B nằm trên đường trung trực của đoạn thẳng AD.
Suy ra BC là đường trung trực của đoạn thẳng AD.
Do đó phát biểu a là đúng.
•Vì BC = BD nên điểm B nằm trên đường trung trực của CD.
Do đó phát biểu c là đúng.
•Vì CB = CD nên điểm C nằm trên đường trung trực của BD.
Do đó phát biểu d là sai.
• Tam giác ABC là tam giác đều nên \(\widehat {ABC} = 60^\circ \)
Trong tam giácABI vuông tại I có \(\widehat {IAB} + \widehat {IBA} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {IAB} = 90^\circ - \widehat {IBA} = 90^\circ - 60^\circ = 30^\circ \).
Xét tam giác ABI có \(\widehat {ABI} > \widehat {IAB}\) (do 60° > 30°).
Suy ra AI > BI (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn)
Do đó điểm I không cách đều hai điểm A và B nên phát biểu b là sai.
Vậy phát biểu a, c là đúng; phát biểu b, d là sai.
