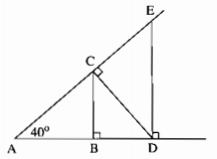
Cho hình dưới:
a) Có bao nhiêu tam giác vuông trong hình?
b) Tính số đo các góc nhọn ở các đỉnh C, D, E.

a) Có năm tam giác vuông trong hình:
∆ABC vuông tại B
∆CBD vuông tại B
∆EDA vuông tại D
∆DCAvuông tại C
Advertisements (Quảng cáo)
∆DCEvuông tại C
b) ∆ABC vuông tại B, suy ra:
\(\widehat A + \widehat {ACB} = 90^\circ \) (tính chất tam giác vuông)
\(\eqalign{
& \Rightarrow \widehat {ACB} = 90^\circ - \widehat A = 90^\circ - 40^\circ = 50^\circ \cr
& \widehat {ACB} + \widehat {BC{\rm{D}}} = \widehat {AC{\rm{D}}} = 90^\circ \cr
& \Rightarrow \widehat {BC{\rm{D}}} = 90^\circ - \widehat {ACB} = 90^\circ - 50^\circ = 40^\circ \cr} \)
∆ACD vuông tại C, suy ra:
\(\widehat A + \widehat {C{\rm{D}}A} = 90^\circ \) (tính chất tam giác vuông)
\(\eqalign{
& \Rightarrow \widehat {C{\rm{D}}A} = 90^\circ - \widehat A = 90^\circ - 40^\circ = 50^\circ \cr
& \widehat {C{\rm{D}}A} + \widehat {C{\rm{D}}E} = \widehat {A{\rm{D}}E} = 90^\circ \cr
& \Rightarrow \widehat {C{\rm{D}}E} = 90^\circ - \widehat {C{\rm{D}}A} = 90^\circ - 50^\circ = 40^\circ \cr} \)
∆DEA vuông tại D, suy ra:
\(\widehat A + \widehat E = 90^\circ \) (tính chất tam giác vuông)
\( \Rightarrow \widehat E = 90^\circ - \widehat A = 90^\circ - 40^\circ = 50^\circ \)
