Cho tam giác ABC có \(\widehat A = 90^\circ \), kẻ AH vuông góc với BC (H ∈ BC). Các tia phân giác của các góc \(\widehat C\) và \(\widehat {BAH}\) cắt nhau ở I. Chứng minh rằng: \(\widehat {AIC} = 90^\circ \)

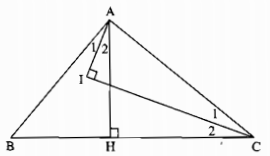
Ta có: \(AH \bot BC\left( {gt} \right) \Rightarrow \Delta AHB\) vuông tại H
Trong tam giác vuông AHB ta có: \(\widehat {AHB} = 90^\circ \)
\( \Rightarrow \widehat B + \widehat {BAH} = 90^\circ \left( 1 \right)\)
Trong tam giác vuông ABC, ta có: \(\widehat {BAC} = 90^\circ \)
\( \Rightarrow \widehat B + \widehat C = 90^\circ \left( 2 \right)\)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra: \(\widehat {BAH} = \widehat C\)
\(\eqalign{
& \widehat {{A_1}} = \widehat {{A_2}} = {1 \over 2}\widehat {BAH}\left( {gt} \right) \cr
& \widehat {{C_1}} = \widehat {{C_2}} = {1 \over 2}\widehat C\left( {gt} \right) \cr} \)
Suy ra: \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{C_1}} = \widehat {{C_2}}\)
\(\widehat {{A_1}} + \widehat {IAC} = \widehat {BAC} = 90^\circ \)
Suy ra: \(\widehat {{C_1}} + \widehat {IAC} = 90^\circ \)
Trong ∆ AIC ta có: \(\widehat {IAC} + \widehat {{C_1}} = 90^\circ \)
Vậy \(\widehat {AIC} = 90^\circ \)
