Chứng minh rằng MA + MB < IA + IB < CA + CB.. Câu 21 trang 40 Sách Bài Tập (SBT) Toán lớp 7 tập 2 - Bài 3: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
Cho hình dưới. Chứng minh rằng MA + MB < IA + IB < CA + CB
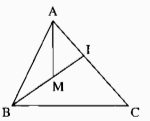

Trong ∆AMI ta có:
MA < MI + IA (bất đẳng thức tam giác)
Cộng vào 2 vế với MB ta có:
MA + MB < MI + IA + MB
Advertisements (Quảng cáo)
\( \Rightarrow \) MA + MB < IB + IA (1)
Trong ∆BIC ta có:
IB < IC + CB (bất đẳng thức tam giác)
Cộng vài 2 vế với IA ta có:
IB + IA < IC + CB + IA
\( \Rightarrow \) IB + IA < CA + CB (2)
Từ (1) và (2) suy ra: MA + MB < IB + IA < CA + CB
