Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm M sao cho MD = MA.
a) Tính số đo góc ABD.
b) Chứng minh:∆ABC = ∆BAD.
c) So sánh độ dài AM và BC.

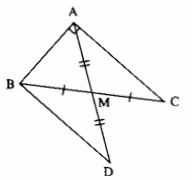
a) Xét ∆AMC và ∆BMD:
BM = MC (gt)
\(\widehat {ABM} = \widehat {BMC}\) (đối đỉnh)
AM = MD (gt)
Do đó: ∆AMC = ∆DMB (c.g.c)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {MAC} = \widehat D\) (2 góc tương ứng)
Suy ra: AC // BD (vì có hai góc ở vị trí so le trong bằng nhau)
\(AB \bot AC\left( {gt} \right)\)
Suy ra \(AB \bot B{\rm{D}}\). Vậy \(\widehat {AB{\rm{D}}} = 90^\circ \)
b) Xét ∆ABC và ∆BAD:
AB cạnh chung
\(\widehat {BAC} = \widehat {AB{\rm{D}}} = 90^\circ \)
AC = BD (Vì ∆AMC = ∆DMB)
Do đó: ∆ABC = ∆BAD (c.g.c)
c) ∆ABC = ∆BAD => BC = AD (2 cạnh tương ứng)
Ta có: \(AM = {1 \over 2}A{\rm{D}}\). Suy ra: \({\rm{A}}M = {1 \over 2}BC\)
