Chứng minh rằng DK = KC.. Câu 36 trang 43 Sách Bài Tập (SBT) Toán lớp 7 tập 2 - Bài 4: Tính chất ba đường trung tuyến của tam giác
Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Trên cạnh BC lấy điểm E sao cho \(BE = {1 \over 3}BC\). Gọi K là giao điểm của AE và CD. Chứng minh rằng DK = KC.

Trong ∆ACD ta có CB là đường trung tuyến kẻ từ đỉnh C.
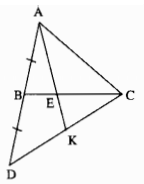
E ∈ BC và \(BE = {1 \over 3}BC\) (gt)
Advertisements (Quảng cáo)
Suy ra: \(CE = {2 \over 3}CB\) nên E là trọng tâm của ∆ACD.
Do đó AK là đường trung tuyến của ∆ACD.
Xuất phát từ đỉnh A nên K là trung điểm của CD.
Vậy KD = KC.
