Cho tam giác ABC, K là trung điểm của AB, E là trung điểm của AC. Trên tia đối của tia KC lấy điểm M sao cho KM = KC. Trên tia đối của tia EB lấy điểm N sao cho EN = EB. Chứng minh rằng A là trung điểm của MN.
Giải
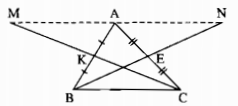
Xét ∆AKM và ∆BKC, có:
AK = BK (gt)
\(\widehat {AKM} = \widehat {BKC}\) (đối đỉnh)
KM = KC (gt)
Suy ra: ∆AKM = ∆ BKC(c.g.c)
\( \Rightarrow \) AM = BC (2 cạnh tương ứng)
\(\widehat {AMK} = \widehat {BCK}\) (2 góc tương ứng)
Suy ra: AM // BC (vì có cặp góc so le trong bằng nhau)
Advertisements (Quảng cáo)
Xét ∆AEN và ∆ CEB, ta có:
AE = CE (gt)
\(\widehat {A{\rm{E}}N} = \widehat {CEB}\) (đối đỉnh)
EN = EB(gt)
Suy ra: ∆AEN = ∆ CEB(c.g.c)
=>AN = BC (2 cạnh tương ứng)
\(\widehat {E{\rm{A}}N} = \widehat {ECB}\) (2 góc tương ứng)
Suy ra: AN // BC (vì có cặp góc so le trong bằng nhau)
Ta có: AM //BC và AN // BC nên hai đường thẳng AM và AN trùng nhau hay M, A, N thẳng hàng. (1)
AM = AN (vì cùng bằng BC) (2)
Từ (1) và (2) suy ra: A là trung điểm của MN.
