Chứng minh rằng AB = CD, AB // CD.. Câu 45 trang 143 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 4: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
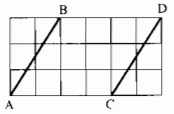
Cho các đoạn thẳng AB và CD trên giấy kẻ ô vuông (hình dưới). Chứng minh rằng AB = CD, AB // CD.

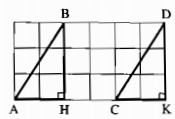
Gọi giao điểm của đường kẻ ô vuông đi qua điểm A và đi qua điểm B cắt nhau tại H ; đi qua điểm C và đi qua điểm D là K.
Xét ∆ AHB và ∆CKD, ta có:
Advertisements (Quảng cáo)
AH = CK (gt)
\(\widehat {AHB} = \widehat {CK{\rm{D}}} = 90^\circ \)
BH = DK (bằng 3 ô vuông)
Suy ra: ∆ AHB = ∆CKD (c. g.c)
\( \Rightarrow \) AB = CD và \(\widehat {BAH} = \widehat {DCK}\)
Hai đường thẳng AB và CD cắt đường thẳng AK có 2 góc \(\widehat {BAH}\) và \(\widehat {DCK}\) ở vị trí đồng vị bằng nhau nên AB // CD.
