Cho tam giác ABC có AB < AC, đường cao AH. Chứng minh rằng:
HB < HC, \(\widehat {HAB} < \widehat {HAC}\) (xét hai trường hợp: \(\widehat B\) nhọn và \(\widehat B\) tù).

a)
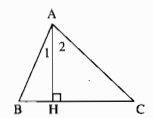
Trường hợp: \(\widehat B < 90^\circ \)
Đường xiên AB < AC nên hình chiếu HB < HC
Trong ∆ABC ta có: AB < AC
\( \Rightarrow \widehat B < \widehat C\) (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ∆AHB có \(\widehat {AHB} = 90^\circ \)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat B + \widehat {HAC} = 90^\circ \) (tính chất tam giác vuông) (1)
Trong ∆AHC có \(\widehat {AHC} = 90^\circ \)
\( \Rightarrow \widehat C + \widehat {HAC} = 90^\circ \) (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: \(\widehat B + \widehat {HAB} = \widehat C + \widehat {HAC}\)
Mà \(\widehat B > \widehat C\) nên \(\widehat {HAB} < \widehat {HAC}\)
b)
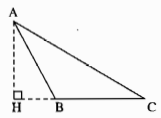
Nếu \(90^\circ < \widehat B < 180^\circ \) điểm B nằm giữa H và C.
\(\widehat {HAC} = \widehat {HAB} + \widehat {BAC}\)
\( \Rightarrow \widehat {HAB} < \widehat {HAC}\)
