Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF (hình dưới)
a) Chứng minh rằng A là trung điểm EF.
b) Các đường cao của tam giác ABC là các đường trung trực của tam giác nào?
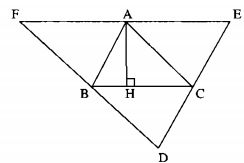

a) Xét ∆ABC và ∆ACE:
\(\widehat {ACB} = \widehat {CA{\rm{E}}}\) (so le trong, AE // BC)
AC cạnh chung
\(\widehat {CAB} = \widehat {AC{\rm{E}}}\) (so le trong, CE // AB)
Do đó: ∆ABC = ∆CEA (g.c.g)
\( \Rightarrow \) AE = BC (1)
Xét ∆ABC và ∆ABF:
\(\widehat {ABC} = \widehat {{\rm{BAF}}}\) (so le trong, BF // AC)
Advertisements (Quảng cáo)
AC cạnh chung
\(\widehat {BAC} = \widehat {ABF}\) (so le trong, BF // AC)
Do đó: ∆ABC = ∆BAF (g.c.g)
\( \Rightarrow \) AF = BC (2)
Từ (1) và (2) suy ra: AE = AF. Vậy A là trung điểm EF.
b) Kẻ \({\rm{A}}H \bot BC\)
EF // BC (gt)
\( \Rightarrow \) \(AH \bot EF\)
AE = AF (chứng minh trên)
Vậy đường cao AH là đường trung trực của EF.
Chứng minh tương tự câu a, ta có B là trung điểm DF và DF // AC nên đường cao kẻ từ đỉnh B của ∆ABC là đường trung trực DFF.
Ta có C là trung điểm DE và DE // AB nên đường cao kẻ từ đỉnh C của ∆ABC là đường trung trực của DE.
