Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất.. Câu 85 trang 53 Sách Bài Tập (SBT) Toán lớp 7 tập 2 - Bài tập ôn chương III - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
Cho bốn điểm A, B, C, D như hình dưới. Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất.
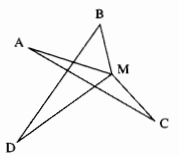

Với M là điểm bất kỳ.
Ta có M không trùng với giao điểm của AC và BD
Trong ∆MBD ta có:
MB + MD > BD (bất đẳng thức tam giác)
Nếu M trùng với giao điểm AC và BD
Advertisements (Quảng cáo)
\( \Rightarrow \) MA + MC = AC
MB + MD = BD
Vậy MA + MC ≥ AC
MB + MD ≥ BD
(dấu bằng xảy ra khi M trùng với giao điểm của AC và BD)
\( \Rightarrow \) MA + MB + MC + MD ≥ AC + BD
Vậy MA + MB + MC + MD = AC + BD bé nhất khi đó M là giao điểm của AC và BD
