Cho hình sau trong đó G là trọng tâm của tam giác ABC. Chứng minh rằng:
a) \({S_{AGC}} = 2{{\rm{S}}_{GMC}}\)
b) \({S_{Gmb}} = {S_{GMC}}\)
c) \({S_{AGB}} = {S_{AGC}} = {S_{BGC}}\)
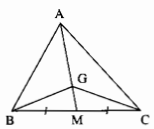

a) G là trọng tâm của ∆ABC
\( \Rightarrow \) GA = 2GM (tính chất đường trung tuyến)
∆AGC và ∆GMC có chung đường cao kẻ từ đỉnh C đến AM.
Cạnh đáy GA = 2GM
Advertisements (Quảng cáo)
Chiều cao chung của hai tam giác
Suy ra: \({S_{AGC}} = 2{{\rm{S}}_{GMC}}\) (1)
b) ∆GMB và ∆GMC có cạnh đáy MB = MC, chung chiều cao kẻ từ đỉnh G đến cạnh BC
\({S_{Gmb}} = {S_{GMC}}\) (2)
c) Hai tam giác AGB và GMB có chung chiều cao kẻ từ đỉnh B đến cạnh AM.
AG = 2GM (chứng minh trên)
Suy ra:
\(\eqalign{
& {S_{AGB}} = 2{{\rm{S}}_{GMB}}\left( 3 \right) \cr
& {S_{BGC}} = {S_{GMB}} + {S_{GMC}} = 2{S_{GMB}}\left( 4 \right) \cr} \)
Từ (1), (2) và (3) suy ra: \({{\rm{S}}_{AGC}} = {S_{AGB}} = {S_{BGC}}\)
