Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây.
a) Trên hình bên trái: AH = 7cm, HC = 2cm
b) Trên hình bên phải: AH = 4cm, HC = 1cm
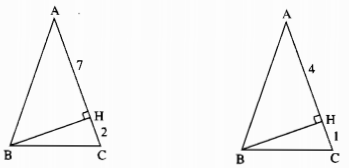

a) ∆ABC cân tại A, ta có: AB = AC = 2 + 7 = 9
Trong tam giác vuông BHA, ta có \(\widehat {BHA} = 90^\circ \)
Áp dụng định lý Pytago, ta có: \(A{H^2} = B{H^2} + H{A^2}\)
Suy ra: \(B{H^2} = A{B^2} - A{H^2} = {9^2} - {7^2} = 81 - 49 = 32\)
Trong tam giác vuông BHC, ta có \(\widehat {BHC} = 90^\circ \)
Áp dụng định lý Pytago, ta có:
Advertisements (Quảng cáo)
\(B{C^2} = B{H^2} + H{C^2}\)
\(B{C^2} = 32 + {2^2} = 36 \Rightarrow BC = 6\)
b) ∆ABC cân tại A nên ta có: AB = AC = 4 +1 = 5
Trong tam giác vuông BHA, ta có: \(\widehat {BAH} = 90^\circ \)
Áp dụng định lý Pytago, ta có: \(A{B^2} = B{H^2} + H{A^2}\)
Suy ra: \(B{H^2} = A{B^2} - H{A^2} = {5^2} - {4^2} = 25 - 16 = 9\)
Trong tam giác vuông BHC, ta có \(\widehat {BHC} = 90^\circ \)
Áp dụng định lý Pytago, ta có:
\(B{C^2} = B{H^2} + H{C^2}\)
\(B{C^2} = 9 + {1^2} = 10 \Rightarrow BC = \sqrt {10} \)
