
Cho tam giác DEF vuông tại D có cạnh DE = 12 cm, cạnh DF = 16 cm.
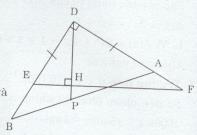
Trên cạnh DF lấy điểm A sao cho DA = DE (A nằm giữa D và F). Trên tia đối của tia ED lấy điểm B sao cho DB = DF (E nằm giữa D và B). Kẻ DH là đường cao của tam giác DEF. Đường thẳng DH cắt AB tại P.
a) Tính độ dài cạnh EF
b) Chứng minh \(\Delta DEF = \Delta DAB\)
c) Chứng minh DP là trung tuyến của tam giác DAB.

a) ∆DEF vuông tại D
Ta có EF2 = DE2 + DF2 (định lí Pythagore)
=> EF2 = 122 + 162 = 400 = 202
=> EF = 20 (cm).
b) Xét ∆DEF và ∆DAB ta có: DE = DA (gt)
\(\widehat D\) (chung)
DF = DB (gt)
Advertisements (Quảng cáo)
Do đó: ∆DEF = ∆DAB (c.g.c).
c) Ta có: \(\widehat {DEF} + \widehat F = 90^\circ\) (∆DEF vuông tại D) và \(\widehat {PDA} + \widehat F = 90^\circ\) (∆DHF vuông tại H)
\( \Rightarrow \widehat {DEF} = \widehat {PDA}\)
Mà \(\widehat {DEF} = \widehat {DAP}\) (∆DEF = ∆DAB). Nên \(\widehat {PDA} = \widehat {DAP}\)
=> ∆DPA cân tại P
Vậy PD = PA (1)
Ta có: \(\widehat {DFE} + \widehat {DEF} = 90^\circ\) (∆DEF vuông tại D)
\(\widehat {BDP} = \widehat {DEF} = 90^\circ\) (∆DEH vuông tại H)
\( \Rightarrow \widehat {DFE} = \widehat {BDP}\)
Mà \(\widehat {DFE} = \widehat {DBP}\) (∆DEF = ∆DAB). Nên \(\widehat {BDP} = \widehat {DBP}\)
=> ∆DBP cân tại P => PA = BP
=> P là trung điểm của AB (\(P \in AB\))
Vậy DP là đường trung tuyến của tam giác DAB.
